Home | Artificial Intelligence Blog
Low-Rank Adaptation (LoRA) was released by Edward Hu and his colleages at Microsoft. The paper was considered game-changing in natural language processing (NLP) field at the time due to its easy implementation and noticeable efficiency.
1. Problem statement
Nowadays, we rarely train a new model from scratch but to take an available pre-trained model and fine-tune it on our datasets. Despite that fine-tuning is significantly faster and less computationally expensive, the cost is still high, especially when model sizes grow.
To tackle that, Edward and his team proposed a technique to cleverly reduce computational cost without affecting the output of the fine-tuning process.
2. Authors’ solution
A neural network contains many dense layers which perform matrix multiplication. The weight matrices in these layers typically have full-rank. When adapting to a specific task, Aghajanyan et al. (2020) shows that the pre-trained language moels have a low “intrinsic dimension” and can still learn efficiently despite a random project to a smaller subspace. Taking advantage of this conclusion, Edward and his team applied it to the fine-tuning phase and found surprisingly good results. For a pre-trained weight matrix $W_0 \in \mathbf{R}^{d \times k}$, they limit its update by adding a component to weights of a layer.
\[h = W_0 x + \Delta W x = W_0x + BAx \quad \text{, where } B \in \mathbf{R}^{d \times r}, A \in \mathbf{R}^{r \times k}\]
In the formula above, the rank $r \ll min(d, k)$.During training, $W_0$ is frozen and does not receive gradient updates, while $A$ and $B$ contain trainable parameters.
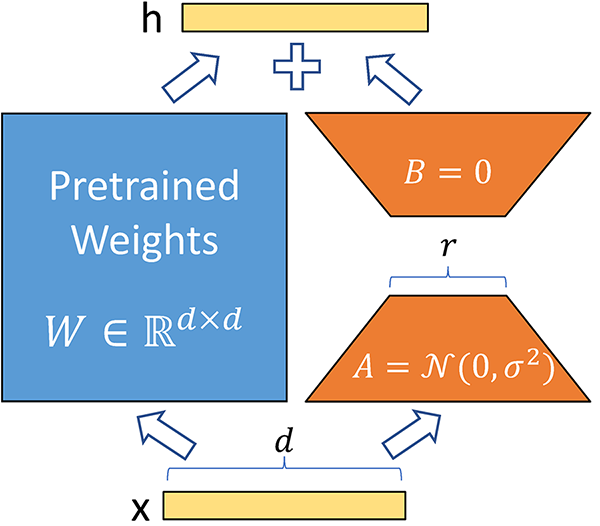
At the start of a fine-tuning scheme, A is sampled from a random Gaussian distribution while B is a zero matrix, so $\Delta W = BA = \mathbf{0}$. Additionally, a constant $\frac{\alpha}{r}$ is introduced to the $\Delta W$. As the constant is not crucial to the fine-tuning, the authors set it to the first rank ($r$) at each experiment (They tried many ranks but kept $\alpha$ fixed at the initial value).
3. Let’s build it
4. Conclusion
1. Problem statement
Edmond is an intellectually outstanding student. One day, he is tasked with measuring heights of all the students in his school. The task requires filling in 3 fields: name, gender, and height. Unfortunately, he forgets the gender column and worries that the teacher might notice and think poorly of him. Being a smart and trustworthy student, Edmond cannot let that happen. Determined to fix the mistake, he searches for an efficient and accurate way to fill in the missing information. That is how he comes across the concept of “Expectation-Maximisation”.
2. Expectation-Maximisation (EM)

In general, the Expectation-Maximisation (EM) algorithm is used to estimate hidden variables or distributions from observed data when some information is incomplete or missing. It iteratively alternates between assigning probabilities to the missing data (Expectation step) and optimizing parameters based on these assignments (Maximisation step).
In Edmond’s case, the observed data consists of the names and heights of the students, while the missing data is the gender. By applying EM, Edmond can infer the gender for each recorded height based on statistical patterns, such as the distribution of heights typically associated with different genders in the school population. This allows him to fill in the missing fields accurately, even though the gender information was initially incomplete.
3. How it works

Given the statistical model which generates a set \(\mathbf{X}\) of observed data, a set of unobserved latent data or missing values \(\mathbf{Z}\), and a vector of unknown parameters \(\theta\), along with a likelihood function \(L(\theta; \mathbf{X}, \mathbf{Z}) = p(\mathbf{X}, \mathbf{Z} \mid \theta)\) the maximum likelihood estimate (MLE) of the unknown parameters is determined by maximising the marginal likelihood of the observed data:
\[L(\theta; \mathbf{X}) = p(\mathbf{X} \mid \theta) = \int p(\mathbf{X}, \mathbf{Z} \mid \theta) p(\mathbf{Z} \mid \theta) \, d\mathbf{Z}.\]
However, this quantity is often intractable since \(\mathbf{Z}\) is unobserved and the distribution of \(\mathbf{Z}\) is unknown before attaining \(\theta\).
The EM Algorithm
The EM algorithm seeks to find the maximum likelihood estimate of the marginal likelihood by iteratively applying these two steps:
Expectation step (E step): Define \(Q(\theta \mid \theta^{(t)})\) as the expected value of the log likelihood function of \(\theta\), with respect to the current conditional distribution of \(\mathbf{Z}\) given \(\mathbf{X}\) and the current estimates of the parameters \(\theta^{(t)}\):
\[Q(\theta \mid \theta^{(t)}) = \mathbb{E}_{Z \sim p(\cdot \mid \mathbf{X}, \theta^{(t)})} \left[ \log p(\mathbf{X}, \mathbf{Z} \mid \theta) \right].\]
Maximization step (M step): Find the parameters that maximize this quantity:
\[\theta^{(t+1)} = \underset{\theta}{\operatorname{arg\,max}} \, Q(\theta \mid \theta^{(t)}).\]
More succinctly, we can write it as one equation:
\[\theta^{(t+1)} = \underset{\theta}{\operatorname{arg\,max}} \, \mathbb{E}_{Z \sim p(\cdot \mid \mathbf{X}, \theta^{(t)})} \left[ \log p(\mathbf{X}, \mathbf{Z} \mid \theta) \right].\]
4. An Hands-on example
One famous algorithm is usually associated with EM is Gaussian Mixture. Basically, Gaussian Mixture is an unsupervised algorithm that is mostly used to cluster data. In this section, in order to give you a better understanding of how EM and Gaussian mixture work, I will use a simple binomial mixture example.

Imagine that you have two coins with unknown probabilities of heads, denoted p and q respectively. The first coin is chosen with probability \(\pi\) and the second is chosen with probability \(1 - \pi\). The chosen coin is flipped once and the result is recorded. \(x = \{1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1\}\) (Heads = 1, Tails = 0). Let \(Z_i \in \{0, 1\}\) denotes which coin was used on each toss.
Applying EM to the example, we start by using binary cross entropy (BCE) to determine the similarity between 2 distributions:
\[Q(\theta \mid \theta^{(t)}) = \mathbb{E} \left[ \sum_{i}^{n}z_i \log(\pi p^{x_i}(1-p)^{1-x_i}) + (1-z_i) \log((1-\pi) q^{x_i} (1-q)^{1-x_i}) \right]\]

1. Introduction to Energy-based models (EBMs)
Energy-based models (EBMs) are a class of probabilistic models that assign an energy to each configuration of the input data and learn to identify low-energy configurations. Unlike traditional supervised learning methods that directly predict output from input, EBMs instead use an energy function to determine stable configurations.
-
Key Concepts:
-
- Energy function: An energy function is a scalar function that maps input configurations to energy values. The goal is to find low-energy configurations, which correspond to stable states or patterns in the data.
-
- State: Each possible configuration of the model (e.g., the activations in a neural network) represents a state.
-
- Energy Minimisation: EBMs learn by finding the lowest-energy states, effectively discovering the most probable or stable states.
-
Why EBMs are relevant:
-
- They offer a flexible approach to model complex distributions without requiring explicit probability calculations.
-
- EBMs have foundational importance in unsupervised learning and associative memory and have influenced many modern architectures.
2. Core concepts of energy-based models
-
Energy functions: In physics, energy represents the system’s potential to perform work. In EBMs, energy functions encode how compatible a given state is with the underlying data distribution. Lower energy means the model is more confident in that state, making energy minimisation a core process.
-
Objective: The primary objective in EBMs is to minimise the energy of states that align with observed data, while pushing non-observed (or less probable) states to higher energies.
-
Connection to physics: EBMs are inspired by concepts from statistical mechanics, where systems evolve towards configurations that minimize free energy. This concept is leveraged to ensure the model “learns” representations by converging to stable, low-energy states.
1. Giới thiệu về reinforcement learning
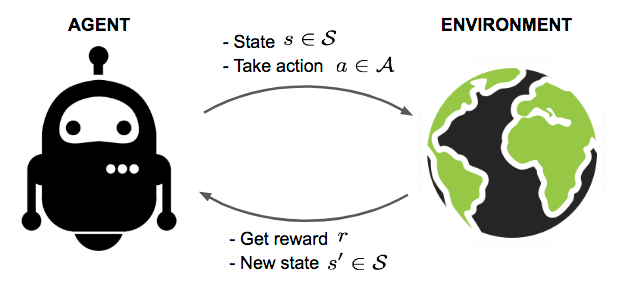
Reinforcement learning là một nhánh đặc biệt của học máy và không thuộc cả 2 loại supervised learning và unsupervised learning. Lý do nó không phải là supervised learning và unsupervised learning là vì phương pháp này không cần đến labels và không được thiết kế để tìm ra cấu trúc ẩn (hidden structure) của dữ liệu. Đây là một giải thuật học bằng trials-and-errors. Trong RL, chúng ta sẽ huấn luyện agent học cách hành động trong một môi trường (environment), ta chỉ cần đặt mục tiêu và agent sẽ tìm ra phương án để đạt được mục tiêu đó.
Xin chào các bạn,
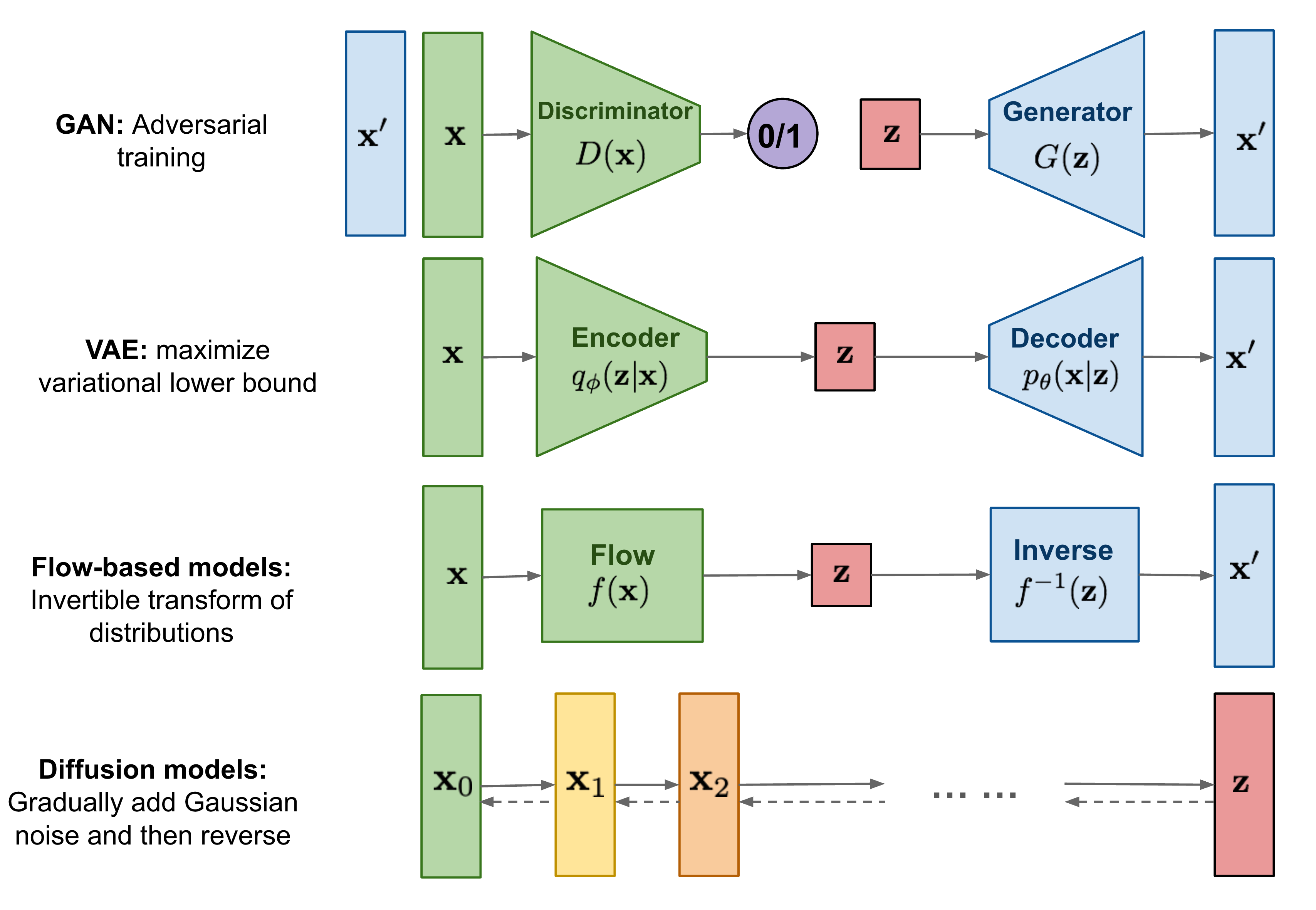
Cho đến nay, mình đã viết về hai loại mô hình sinh dữ liệu, gồm GANs và VAE. Chúng đã cho thấy thành công lớn trong việc tạo ra các hình ảnh có chất lượng rất tốt, nhưng mỗi loại đều có những hạn chế riêng. Mô hình GAN thường gặp phải vấn đề bất ổn trong quá trình training và thiếu đa dạng trong quá trình sinh dữ liệu do bản chất adversarial learning của nó. VAE dựa vào một hàm loss xấp xỉ (surrogate loss).
Mô hình Diffusion được lấy cảm hứng từ nhiệt động học phi cân bằng (Non-equilibrium thermodynamics). Chúng áp dụng Markov chain của các bước khuếch tán nhằm dần dần thêm random noise vào data, sau đó học cách đảo ngược quá trình khuếch tán để tạo ra các mẫu dữ liệu mong muốn từ nhiễu. Không giống như GANs và VAE, mô hình Diffusion được huấn luyện theo một quy trình cố định và latent dimension có dimension bằng với data.
1. Mô hình Diffusion là gì và nó hoạt động như thế nào ?
Xin chào các bạn,
Trong bài post này, mình sẽ giải thích về toán học và code Support Vector Machine.

1. Giới thiệu
Support Vector Machine là một giải thuật phân loại có giám sát (supervised learning) được đề xuất bởi nhà khoa học người Liên Xô Vladimir Vapnik và các cộng sự. Đây là một giải thuật cực kì thú vị cho các bạn mới học ML/AI vì cách diễn giải và chứng minh toán học không quá phức tạp nhưng cực kì hiệu quả.
Ban đầu, giải thuật này chỉ được sử dụng cho việc phân loại 2 classes (binary classification). Tuy nhiên, sau đó cộng đồng AI/ML đã cải biến để có thể dùng nó cho multiple-class classification, regression.
2. Giải thích toán học
Các lý thuyết về của SVM bao quanh các định lý cơ bản của toán học như vector, matrix, tối ưu Larange.
Primal form của SVM có dạng như sau:
\[\min_{w, b} \frac{1}{2}||w|| + C \sum_{1}^{n}{\xi_i}\]
Xin chào các bạn,
Trong bài post này, mình sẽ trình bày về một giải thuật dùng để giảm chiều dữ liệu có tên là Principle Component Analysis (PCA). Đây là một giải thuật khá cổ tuy nhiên những giá trị toán học nó mang lại vẫn trường tồn theo thời gian. Chúng ta hãy cùng khám phá xem nó hoạt động như thế nào nhé.
1. Giới thiệu
Như đã đề cập ở tiêu đề, PCA là một giải thuật dùng để giảm chiều của dữ liệu trong khi tối thiểu thông tin mất mát. Nó có rất nhiều ứng dụng thực tế như:
- Visualise data
- Data Compression
*
Xin chào các bạn,
Trong bài post này, mình sẽ giới thiệu về nén data (data compression).
1. Giới thiệu
Nếu các bạn dùng máy tính, chắc chắn đã từng thấy từ “Compress file” khi right click vào một folder nào đó. Compress file này tức là mã hóa (encode) folder này lại thành một đoạn code có thể được giải mã với ít bits hơn nhằm giảm dung lượng lưu trữ của chúng để có thể dễ dàng di chuyển.
Vì vậy, nén data là lĩnh vực dùng các giải thuật để có thể mã hóa dữ liệu thành một đoạn dữ liệu có dung lượng nhỏ hơn và có thể giải mã để lấy lại dữ liệu gốc khi ta muốn. Data compression được chia thành 2 nhóm chính: lossy compression và lossless compression. Lossy compression là giải thuật nén ảnh làm mất một phần nào đó của dữ liệu gốc và lossless là giải thuật nén ảnh mà không làm mất dữ liệu gốc.
- Những khác biệt chính giữa lossy và lossless compression
| |
Lossy |
Lossless |
| Chất lượng |
Mất mát 1 phần |
Không mất |
| Applications |
Ảnh, videos, nhạc |
Ảnh, videos, nhạc, text |
| File types |
Images: JPEG |
Images: RAW, BMP, PNG |
| |
Video: MPEG, AVC, HEVC |
General: ZIP |
| |
Audio: MP3, AAC |
Audio: WAV, FLAC |
 Hình 1.1. Lossy vs Lossless compression
Hình 1.1. Lossy vs Lossless compression
Xin chào các bạn,
Xin chào các bạn,
Trong bài post này, mình sẽ giải thích về các công thức toán học Wasserstein GAN (WGAN) và code kiến trúc này from scratch với Pytorch.
1. Giới thiệu
WGAN là một kiến trúc tạo sinh (generative model) giống như GAN truyền thống với một vài sự thay đổi về hàm loss để cải thiện performance. Như các bạn đã biết, việc huấn luyện GAN truyền thống sẽ gặp rất nhiều khó khăn như collapse mode, non-convergence, diminished gradient, unbalance training, sensitive to hyperparameters, … Các bạn có thể đọc thêm bài viết của Jonathan Hui để biết thêm chi tiết về các nhược điểm của GANs truyền thống, trong post của tác giả có liệt kê đầy đủ và giải thích chi tiết các nhược điểm cố hữu của GANs truyền thống.
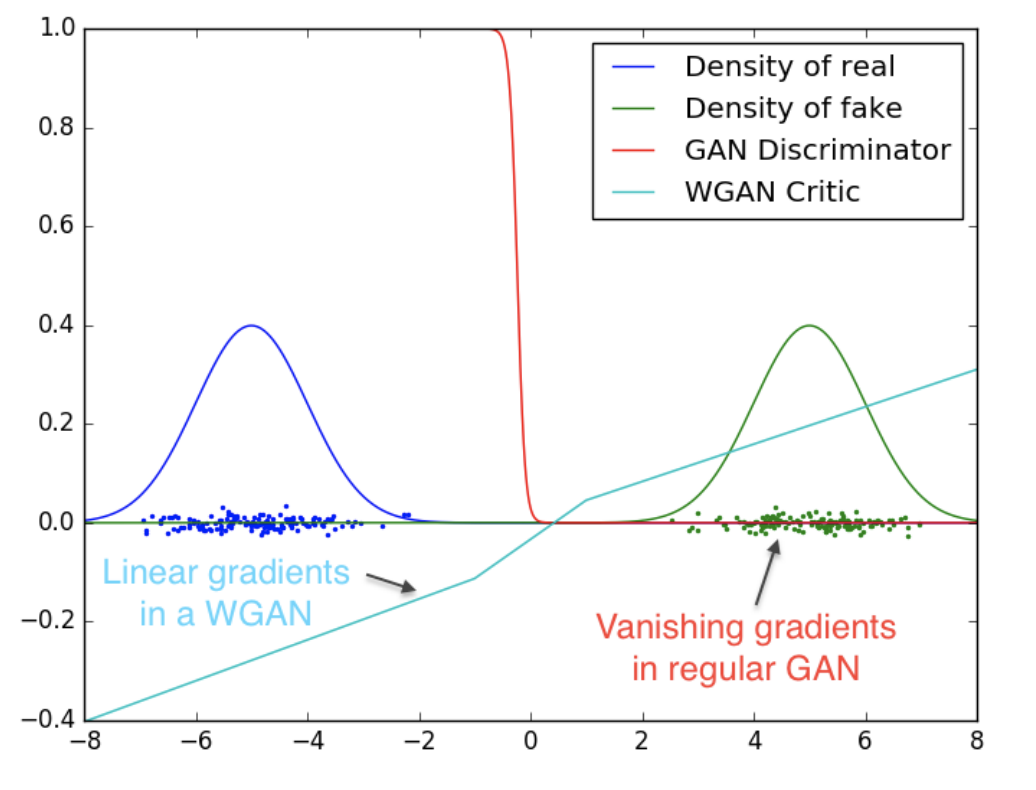
Xin chào các bạn!
Trong bài post này, mình sẽ giới thiệu về mô hình Variational AutoEncoder được công bố trong paper “Auto-Encoding Variational Bayes” của tác giả Diederik P. Kingma và các cộng sự. Đây là một kiến trúc tương tự như AutoEncoder và có thêm thành phần stochastic trong phần bottleneck để khiến cho nó có khả năng tạo ra những data mới lạ (tuy vẫn thuộc distribution của training dataset).
1. Giới thiệu
GANs (Generative Adversarial Networks) được giới thiệu lần đầu vào năm 2014 trong bài báo “Generative Adversarial Nets” của Ian J. Goodfellow và các cộng sự. Đây là một phương pháp học không giám sát (unsupervised learning) được sử dụng để tạo ra dữ liệu mới mang tính chân thực và đa dạng.
 Hình 1.1. Tất cả gương mặt trên đều được tạo bởi GANs
Hình 1.1. Tất cả gương mặt trên đều được tạo bởi GANs
Mô hình GANs có kiến trúc cực kỳ thú vị, bao gồm hai mạng chính: Generator và Discriminator, hoạt động theo cơ chế đối kháng. Generator cố gắng tạo ra dữ liệu giả mạo giống như dữ liệu thật, trong khi Discriminator cố gắng phân biệt giữa dữ liệu thật và dữ liệu giả. Qua quá trình huấn luyện, cả hai mạng này đều cải thiện chất lượng của mình, dẫn đến việc tạo ra dữ liệu giả ngày càng chân thực hơn.
1. Giới thiệu
Naive Bayes Classifier là một thuật toán phân loại dựa trên định lý Bayes, với giả định quan trọng là các đặc trưng của dữ liệu đều độc lập có điều kiện với nhau. Dù giả định này có thể không hoàn toàn đúng trong nhiều trường hợp, Naive Bayes vẫn hoạt động hiệu quả trong nhiều ứng dụng thực tế, đặc biệt là các bài toán phân loại văn bản như phát hiện spam, phân tích cảm xúc, và phân loại tài liệu.
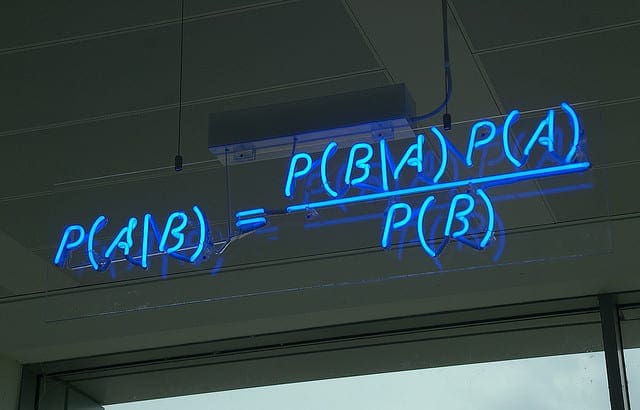
Naive Bayes được ưa chuộng nhờ vào sự đơn giản trong cài đặt, tốc độ nhanh chóng khi xử lý dữ liệu lớn, và khả năng mở rộng cho nhiều loại dữ liệu khác nhau. Trong bài viết này, chúng ta sẽ đi sâu vào phần toán học phía sau Naive Bayes, các biến thể phổ biến của nó, và phân tích ưu và nhược điểm của phương pháp này.
2. Naive Bayes Classifier - Phần toán
2.1. Định lý Bayes
Naive Bayes Classifier dựa trên định lý Bayes, công thức tổng quát như sau:
\[P(C \mid X) = \frac{P(X \mid C) \cdot P(C)}{P(X)}\]
Thuật toán Naive Bayes tính xác suất của từng class cho một mẫu dữ liệu mới, và chọn class có xác suất cao nhất làm kết quả phân loại. Điểm quan trọng là giả định Naive Bayes đưa ra: các đặc trưng \(X_i\) là độc lập có điều kiện dựa trên class \(C\). Điều này cho phép công thức được viết lại dưới dạng:
\[P(C \mid X_1, X_2, ..., X_n) \propto P(C) \cdot \prod_{i=1}^{n} P(X_i \mid C)\]
2.2. Gaussian Naive Bayes
Gaussian Naive Bayes (GNB) được sử dụng khi các feature là số và giả định rằng các đặc trưng này tuân theo phân phối Gauss. Với GNB, xác suất \(P(X_i \mid C)\) được tính bằng hàm mật độ xác suất của phân phối Gaussian:
\[P(X_i \mid C) = \frac{1}{\sqrt{2\pi \sigma_{iC}^2}}exp(-\frac{(X_i - \mu_{iC})^2}{2\sigma_{iC}^2})\]
Trong đó, \(\mu_{iC}\) và \(\sigma_{iC}^2\) là trung bình và phương sai của phân phối Gauss của feature đó trong class \(C\).
2.3. Multinomial Naive Bayes
Multinomial Naive Bayes (MNB) chủ yếu được sử dụng cho các bài toán phân loại văn bản, nơi dữ liệu được biểu diễn dưới dạng tần suất hoặc xác suất xuất hiện của các từ (hoặc đặc trưng) trong một tài liệu. Với MNB, xác suất \(P(X_i \mid C)\) được tính dựa trên tần suất xuất hiện của từ \(X_i\) trong các tài liệu thuộc class \(C\):
\[P(X_i \mid C) = \frac{N_{iC} + \alpha}{N_C + \alpha \vert V \vert}\]
Trong đó,
* \(N_{iC}\) : tổng số lần xuất hiện của \(X_i\) trong các tài liệu thuộc class \(C\)
* \(N_C\): tổng số từ trong các tài liệu ở class \(C\)
* \(\vert V \vert\): kích thước từ vựng
* \(\alpha\): giá trị làm mượt để tránh bị probability = 0, thường sử dụng Laplace smoothing với \(\alpha = 1.\)
2.4. Complement multinomial Naive Bayes
Complement Naive Bayes (CNB) là một biến thể của MNB, đặc biệt hữu ích cho các tập dữ liệu mất cân bằng. Thay vì tính xác suất \(P(X_i \mid C)\) trực tiếp cho một class, CNB tính xác suất của từ $X_i$ trong tất cả các class khác ngoài class \(C\). Điều này giúp CNB hoạt động tốt hơn khi có sự chênh lệch lớn giữa các class.
Công thức của CNB:
\[P(X_i \mid C) = \frac{N_{i \overline{C}} + \alpha}{N_{\overline{C}} + \alpha|V|}\]
Trong đó,
* \(N_{i \overline{C}}\): tổng số lần xuất hiện của \(X_i\) trong các tài liệu không thuộc class \(C\).
* \(N_{\overline{C}}\): tổng số từ trong các tài liệu không thuộc class \(C\).
* \(\vert V \vert\): kích thước từ vựng.
* \(\alpha\): giá trị làm mượt để tránh bị probability = 0, thường sử dụng Laplace smoothing với \(\alpha = 1.\).
3. Ưu và nhược
Ưu điểm
-
Đơn giản và dễ triển khai
-
Không yêu cầu nhiều dữ liệu huấn luyện
-
Xử lý tốt cả dữ liệu số (numerical) và
-
Thời gian xử lý nhanh
-
Ít bị ảnh hưởng bởi các feature không liên quan (curse of dimensionality)
Nhược điểm
-
Naive Bayes giả định rằng tất cả các đặc trưng (hoặc yếu tố dự báo) là độc lập, điều này hiếm khi xảy ra trong thực tế. Điều này giới hạn tính ứng dụng của thuật toán trong các trường hợp thực tế.
-
Các ước lượng của nó có thể không chính xác trong một số trường hợp, vì vậy không nên quá tin tưởng và dùng vào các giá trị xác suất mà nó trả về để tham dự các cuộc thi hoặc viết papers.
Xin chào các bạn,
Trong bài post này, mình sẽ giới thiệu về chuỗi Fourier và biến đổi Fourier. Đây là một giải thuật có rất nhiều công dụng trong Vật lý, toán học, kỹ thuật viễn thông, kỹ thuật tự động, … Ngoài ra, biến đổi Fouier có thể có rất rất nhiều ứng dụng ngoài đời thật. Vì nó rất quan trọng và có rất nhiều thứ ta có thể áp dụng nó nên mình sẽ đi sâu vào việc chứng minh nó để có thể giúp các bạn hiểu được giải thuật này hoạt động như thế nào.

Xin chào các bạn,
Trong bài post về các bộ lọc phần 2, mình đã giới thiệu về các bộ lọc cạnh và cũng như cách hoạt động của chúng. Ở phần này, mình sẽ giới thiệu một giải thuật cho kết quả vượt trội hơn các phương pháp trước có tên là Canny edge detection. Giải thuật này được phát triển bởi John F. Canny vào năm 1986. Nó bao gồm nhiều bước hậu xử lý để có thể cải thiện kết quả so với các phương pháp dựa vào đạo hàm.
1. Điểm yếu của việc dùng đạo hàm để tìm cạnh
Các bộ lọc như Sobel, Prewitt, Laplacian dựa vào mỗi giá trị gradient của pixel để tìm ra cạnh. Tuy nhiên, trong ảnh thu được từ camera sẽ có rất nhiều nguồn nhiễu từ cả bên ngoài và bên trong, và điều này khiến cho các phương pháp này kém ổn đỉnh.
2. Giải thuật Canny
Giải thuật Canny về cơ bản bao gồm 5 bước. Chúng ta hãy cùng xem giải thuật này hoạt động như thế nào và code nó from scratch nhé.
Bước 1: Giảm nhiễu
Để có thể giảm noise và tìm ra các cạnh đáng tin cậy, một bộ lọc thông thấp với mục đích làm mịn ảnh sẽ được áp dụng.
Bộ lọc có thể tùy ý lựa chọn, các bạn có thể chọn bộ lọc trung bình, trung vị, Gauss, bilateral, … miễn là nó làm mịn ảnh. Ở đây mình sẽ dùng Gaussian filter để demo.
import cv2
import matplotlib.pyplot as plt
import numpy as np
# Read image and turn into gray
# Can be replaced with any image
# Step 1: Gaussian Blur
image = cv2.imread("./lena.png", 0)
blurred = cv2.GaussianBlur(image)

Bước 2: Tính gradient và orientation
Ở bước này, ta sẽ dùng các bộ lọc như ở bài này để có tìm ra được các cạnh trong tấm ảnh. Các bạn có thể dùng bất kì bộ lọc gradient-based nào để tìm cạnh cũng được nhé.
Ở bước này, ta cần tính cường độ và hướng gradient tăng nhanh nhất (hướng của cạnh). Và điều này được tính theo công thức sau:
\[G = \sqrt{G_x^2 + G_y ^2}\]
\[\theta = arctan(\frac{G_y}{G_x})\]
# Step 2: Find all edges
def sobelFilter(image):
image_ = image.copy()/255.
Gx = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]], dtype = np.float32)
Gy = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]], dtype = np.float32)
Ix = cv2.filter2D(image_, ddepth=-1, kernel = Gx)
Iy = cv2.filter2D(image_, ddepth=-1, kernel=Gy)
G = np.hypot(Ix, Iy)
G = G/G.max()
theta = np.arctan2(Iy, Ix)
return G, theta/np.pi * 180
G, theta = sobelFilter(blurred)
Xin chào các bạn,
Nối tiếp series phần 1 của bộ lọc, bài post này sẽ giới thiệu thêm một vài bộ lọc nâng cao hơn của phần 1 với trọng tâm chính là tìm cạnh trong ảnh (edge detection).

Xin chào các bạn,
Trong phần 1 của series bộ lọc ảnh, mình sẽ giới thiệu về bộ lọc ảnh, ứng dụng, và một vài bộ lọc ảnh cơ bản nhất trong lĩnh vực xử lý ảnh, thị giác máy.
Xin chào các bạn,
Trong bài post này, mình sẽ hướng dẫn tính thủ công số lượng parameters trong các mạng tích chập.
Xin chào các bạn!
Trong bài post này mình sẽ giới thiệu về kiến trúc VGG, một trong những kiến trúc lâu đời nhất của mạng tích chập. Thật tình cờ, vào thời điểm viết bài blog này cũng là tròn 10 năm ngày ra mắt của mô hình này. Vậy, VGG có gì đặc biệt và có ảnh hưởng đến cách xây dựng các mô hình CNNs sau này như thế nào, chúng ta cùng khám phá nhé.
Xin chào các bạn!
Trong bài post này, mình sẽ giải thích về một vài phương pháp resize ảnh thông dụng nhất trong lĩnh vực computer vision. Chúng ta thường dùng các thư viện có sẵn trong cv2, pytorch, tensorflow, PIL, … để resize ảnh nhưng phương pháp nào phù hợp nhất với nhu cầu cũng như phương pháp nào nhanh nhất, việc này chỉ có thể biết được khi chúng ta hiểu được thuật toáncủa nó và đó cũng chính là mục đích của bài post này.
Xin chào các bạn!
Trong bài post này, mình sẽ giới thiệu về kiến trúc transformers. Đây được xem là một trong những model có tính cách mạng nhất trong deep learning vì nó đã tạo tiền đề cho sự ra đời của các mô hình ngôn ngữ lớn hay các mô hình SOTA cho các task như speech recognition, computer vision, …
Mô hình này được ra mắt nhằm thay thế cho kiến trúc Recurrent neural networks (RNNs), vốn đã được ra mắt vào những năm 90. Sơ lược thì kiến trúc recurrent này được thiết kế ra nhằm xử lý các loại thông tin có thứ tự như text, speech. Tuy nhiên, kiến trúc này có nhược điểm là vấn đề về exploding/vanishing gradient khi training nên nó không thể xử lý một đoạn thông tin quá dài. Vì những lý do đó mà Large language models không tồn tại trước khi transformer được ra mắt.
Đến năm 2014, một nhóm nghiên cứu ở Google đã nghiên cứu những phương pháp để khắc phục vấn đề trên của RNNs và đề xuất kiến trúc transformers. Chỉ sau 10 năm ra mắt, những thành tựu đạt được từ kiến trúc transformers nhiều không xuể với sự ra mắt của các mô hình ngôn ngữ lớn như ChatGPT, Llama3, Segment Anything, …
Xin chào các bạn!
Trong bài post này, mình sẽ giải ngố về giải thuật non-maximum suppression (NMS) thường được dùng trong khâu post-processing của YOLO models.
Xin chào các bạn,
Trong bài post này, mình sẽ giới thiệu một thuật toán image filtering mới tên là Guided Image Filtering. Đây là thuật toán làm mịn ảnh tốt nhất tính đến thời điểm bài post này được viết. Phương pháp này được đề xuất bởi Kaiming He (cũng là cha đẻ của mô hình ResNet), Jian Sun, và Xiaoou Tang tại hội nghị ECCV 2010. Cũng đã thấm thoát 14 năm trôi qua, đã có nhiều biến thể của thuật toán này như Fast Guided Image Filtering, Deep Guided Image filtering, … được đề xuất, tuy nhiên chúng đều dựa trên nền của giải thuật gốc. Đây là một giải thuật đạt được cùng một lúc cả hai tiêu chí: nhanh hơn và tốt hơn.
1. Tại sao Guided Image Filtering được ra đời ?
Thuật toán Guided Image Filtering ra đời với mục tiêu giải quyết một số thách thức quan trọng trong xử lý ảnh, đặc biệt là trong việc làm mịn ảnh. Trước đó, các phương pháp truyền thống như bộ lọc trung bình, Gaussian Blur, bilateral filter lọc nhiễu và làm mịn ảnh nhưng đồng thời cũng làm mất các chi tiết trong ảnh. Để khắc phục nhược điểm đó của các bộ lọc trên, bộ lọc Guided filter tích hợp thêm thông tin của ảnh gốc để có thể “hướng dẫn” giải thuật lọc đi đúng hướng và giữ được nhiều chi tiết nhất có thể.
Ngoài ứng dụng làm mịn, Guided filter còn có thể được ứng dụng cho colorisation, image matting, multi-scale decomposition, và haze removal.
 Ứng dụng của guided filter trong image matting. Nguồn: claude_ssim.log
Ứng dụng của guided filter trong image matting. Nguồn: claude_ssim.log
Xin chào các bạn!
Trong bài post lần này mình sẽ giới thiệu một phương pháp để có thể tự động tải các videos/shorts/livestream từ Youtube về để có thêm nguồn data cho mô hình AI/ML.
Trong lĩnh vực AI/ML, data chiếm 80% công việc của các kĩ sư nên việc biết tận dụng các nền tảng trực tuyến để có thể kiếm thêm nhiều data sẽ rất có ích cho việc xây dựng một mô hình tốt. Có thể kể đến một vài nền tảng nổi tiếng để chúng ta scrape dữ liệu như Instagram, Tiktok, Reddit, Twitter (X), …
Chúng ta bắt tay vào thực hành luôn nhé!
Bước 1: Install thư viện scrapetube, youtube-dl với pip
Cho bạn nào chưa biết, pip là một package manager của Python, nó giúp cho việc cài cắm đơn giản hơn rất nhiều so với việc ta tự download và install thủ công.
Package đầu tiên chúng ta sẽ cài là scrapetube, thư viện này sẽ giúp chúng ta trích xuất urls của các videos/shorts một cách tự động mà không cần phải mở một trình duyệt phụ như thư viện Selenium. Vì vậy, việc dùng thư viện này sẽ tiết kiệm khá nhiều thời gian và băng thông mạng của các bạn 😄. Package thứ hai và cũng là package cuối cùng là youtube_dl, thư viện này sẽ giúp chúng ta tải về các Youtube urls đã được trích xuất dùng.
Xin chào các bạn,
Trong bài post này, mình sẽ giới thiệu một phương pháp để xác định độ quan trọng của từng từ trong một câu.

Vậy mức độ quan trọng của một từ là gì? Mức độ quan trọng ở đây là một con số cụ thể nào đó và nếu nó lớn thì tức là tư đó quan trọng và ngược lại. Giả sử, bài phát biểu nhậm chức của tổng thống Mỹ như sau: “Tôi sẽ tập trung vào y tế”, thì trong câu sau từ “y tế” nên có mức độ quan trọng lớn hơn các từ như “Tôi”, “sẽ”, “tập”, “trung”, “vào”.
1. Giới thiệu TF-IDF
Như tiêu đề thì TF-IDF là từ viết tắt của cụm Term Frequency - Inverse Document Frequency. Giả thuật này được hai nhà khpa học máy tính Hans Peter Luhn và Karen Spärck Jones tìm ra. Cụ thể hơn, Hans là người phát triển phần term frequency và Karen là người thêm phần Inverse Document Frequency vào giải thuật.
2. Giải thuật
Trước khi đi vào công thức, mình muốn làm rõ các terminologies trước.
-
Documents (D): Là tập hợp tất cả những document. Ví dụ [[“Tôi”, “tên”, “A”], [“Tôi”, “là”, “B”]]
-
N: Tổng số lượng các documents. Ví dụ, N = 2 trong trường hợp này.
-
Term (t): Từ. Ví dụ “Tôi, “tên, …
1. Introduction: Real-Life Approximation
Imagine you are coding an algorithm in a low-level programming language, such as Assembly, which lacks built-in functions for calculating trigonometric and exponential values.
Unlike Python, where such calculations are effortless thanks to prebuilt libraries, low-level programming demands a different approach. In this scenario, how can you solve the problem ?
The answer lies in Function Approximation
2. Taylor Approximation
2.1. What is Taylor Approximation
The Taylor approximation represents a function as a polynomial expanded around a specific point. This method is based on the idea that a smooth function can be closely approximated by a sum of its derivatives at a point.
The Taylor series of a function \(f(x)\) around \(x = a\) is given by:
\[f(x) \approx T_n(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n\]
For simplicity, if \((a = 0)\), this becomes the Maclaurin series:
\(T_n(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \cdots + \frac{f^{(n)}(0)}{n!}x^n\)
2.2. Mathematical Proof
According to fundamental theorem of calculus (F.T.C), we have:
\[f(x) = \int_{x_0}^{x} f'(x_1)dx_1 + f(x_0)\]
Expand the F.T.C, we have:
\[\begin{aligned}
f(x) &= \int_{x_0}^{x} \int_{x_0}^{x_1} f''(x_2)dx_2 dx_1 + f(x_0) + \int_{x_0}^{x}f'(x_0)dx_1 \\
&= \int_{x_0}^{x} \int_{x_0}^{x_1} \int_{x_0}^{x_2} f'''(x_3)dx_3 dx_2 dx_1 + f(x_0) + \int_{x_0}^{x}f'(x_0)dx_1 + \int_{x_0}^{x} \int_{x_0}^{x_1} f''(x_0)dx_2 dx_1 \\
&= \int_{x_0}^{x} ... \int_{x_0}^{x_{n-1}} f^{(n)}(x_n)dx_n dx_{n-1}... dx_2 dx_1 + f(x_0) + ... + \frac{1}{n!} f^{(n)}(x - x_0)^n
\end{aligned}\]
Coin \(O_1(n) = \int_{x_0}^{x} ... \int_{x_0}^{x_{n-1}} f^{(n)}(x_n)dx_n dx_{n-1}... dx_2 dx_1\), \(O_2(n) = f(x_0) + ... + \frac{1}{n!} f^{(n)}(x - x_0)^n\). We have:
\[f(x) = O_1(n) + O_2(n)\]
The \(O_1(n)\), which comprises nested integrals, is a complete nightmare. In contrast, the rest of the equation is quite straightforward.
However, the more we expand the equation, the less important is the first term. Let me prove it.
Assume that:
\[\vert f^{(n)}(x_n) \vert \leq b\]
Then,
\[\begin{aligned}
\vert \int_{x_0}^{x} ... \int_{x_0}^{x_{n-1}} f^{(n)}(x_n)dx_n dx_{n-1}... dx_2 dx_1 \vert &\leq \vert f^{(n)}(x_n) \vert \times \vert \int_{x_0}^{x} ... \int_{x_0}^{x_{n-1}}dx_n dx_{n-1}... dx_2 dx_1 \vert \\
& \leq b \times \frac{(x-x_0)^n}{n!}
\end{aligned}\]
If we expand it further,
\[\lim_{n \rightarrow \infty} b \times \frac{(x-x_0)^n}{n!} = 0\]
However, in some cases where \(\vert f^{(n)}(x_n) \vert \leq n^n\). Then we will have
\[\lim_{n \rightarrow \infty} n^n \times \frac{(x-x_0)^n}{n!} \approx (x-x_0)^n\]
This will converge if \(\vert x - x_0 \vert \leq 1\). So you better pick \(x\) that is within 1 unit from the \(x_0\).
Xin chào các bạn,
Trong bài post này, mình sẽ giới thiệu một phương pháp “cổ điển” để extract features của một bức ảnh. Ở thời đại Deep Learning phát triển vượt bậc như hiện nay, các mạng CNN thường được dùng để trích xuất các đặc trưng của bức ảnh. Tuy nhiên, trước khi Yan LeCun đề xuất kiến trúc CNN thì cũng đã có nhiều nghiên cứu về phương pháp để trích xuất features của một bức ảnh và một trong những phương pháp phổ biến nhất đó là Histogram of Oriented Gradients (HOG). Chúng ta hãy cùng tìm hiểu xem HOG là gì và hoạt động như thế nào nhé.

1. Giới thiệu về HOG
HOG là một giải thuật trích xuất những điểm đặc trưng trong một bức ảnh và những đặc trưng này có thể được dùng để đưa vào các mô hình phân loại như SVM, Decision Tree, … cho các task classification, detection, hay thậm chí segmentation.
Điểm chính trong nguyên lý hoạt động c ủa HOG là mô tả hình dạng của một vật thể cục bộ thông qua hai ma trận: magnitude gradient và *orientation gradient. Để tạo ra hai ma trận này, ảnh được chia thành một lưới ô vuông, trên mỗi ô vuông, ta tính toán biểu đồ histogram thống kê độ lớn gradient. Mỗi ô vuông thường có kích thước 8x8 pixels và bao gồm nhiều ô cục bộ. HOG descriptor được tạo thành bằng cách nối liền 4 vector histogram từ mỗi ô cục bộ. HOG descriptor được tạo thành bằng cách nối liền 4 vector histogram từ mỗi ô cục bộ thành một vector tổng hợp. Để cải thiện độ chính xác, mỗi giá trị của vector histogram trên mỗi vùng cục bộ được chuẩn hóa theo Norm 2 hoặc Norm 1. Ưu điểm của HOG là nó bao gồm tính bất biến đối với biến đổi hình học và thay đổi độ sáng, cũng như khả năng loại bỏ chuyển động cơ thể trong phát hiện con người nếu họ duy trì tư thế đứng thẳng.
2. Cách hoạt động của HOG
Ở mục 1, mình đã giới thiệu tổng quan về HOG. Giờ thì hãy cùng đào sâu xem nó được hoạt động như thế nào nhé.