Low-Rank Adaptation (LoRA) was released by Edward Hu and his colleages at Microsoft. The paper was considered game-changing in natural language processing (NLP) field at the time due to its easy implementation and noticeable efficiency.
1. Problem statement
Nowadays, we rarely train a new model from scratch but to take an available pre-trained model and fine-tune it on our datasets. Despite that fine-tuning is significantly faster and less computationally expensive, the cost is still high, especially when model sizes grow.
To tackle that, Edward and his team proposed a technique to cleverly reduce computational cost without affecting the output of the fine-tuning process.
2. Authors’ solution
A neural network contains many dense layers which perform matrix multiplication. The weight matrices in these layers typically have full-rank. When adapting to a specific task, Aghajanyan et al. (2020) shows that the pre-trained language moels have a low “intrinsic dimension” and can still learn efficiently despite a random project to a smaller subspace. Taking advantage of this conclusion, Edward and his team applied it to the fine-tuning phase and found surprisingly good results. For a pre-trained weight matrix $W_0 \in \mathbf{R}^{d \times k}$, they limit its update by adding a component to weights of a layer.
\[h = W_0 x + \Delta W x = W_0x + BAx \quad \text{, where } B \in \mathbf{R}^{d \times r}, A \in \mathbf{R}^{r \times k}\]
In the formula above, the rank $r \ll min(d, k)$.During training, $W_0$ is frozen and does not receive gradient updates, while $A$ and $B$ contain trainable parameters.
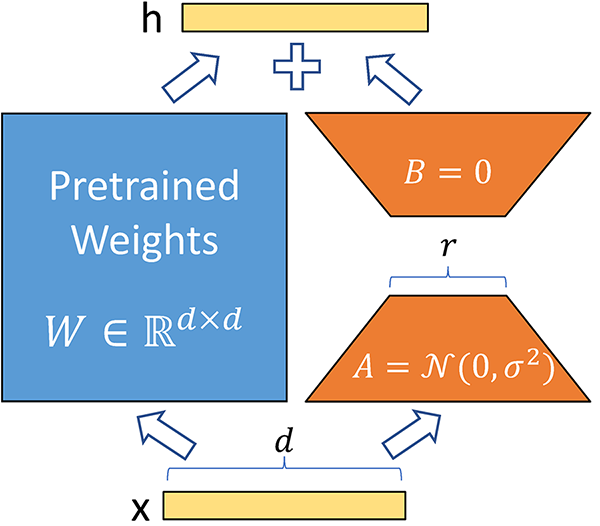
At the start of a fine-tuning scheme, A is sampled from a random Gaussian distribution while B is a zero matrix, so $\Delta W = BA = \mathbf{0}$. Additionally, a constant $\frac{\alpha}{r}$ is introduced to the $\Delta W$. As the constant is not crucial to the fine-tuning, the authors set it to the first rank ($r$) at each experiment (They tried many ranks but kept $\alpha$ fixed at the initial value).
3. Let’s build it
4. Conclusion