Naive Bayes

May 10, 2024

1. Giới thiệu

Naive Bayes Classifier là một thuật toán phân loại dựa trên định lý Bayes, với giả định quan trọng là các đặc trưng của dữ liệu đều độc lập có điều kiện với nhau. Dù giả định này có thể không hoàn toàn đúng trong nhiều trường hợp, Naive Bayes vẫn hoạt động hiệu quả trong nhiều ứng dụng thực tế, đặc biệt là các bài toán phân loại văn bản như phát hiện spam, phân tích cảm xúc, và phân loại tài liệu.

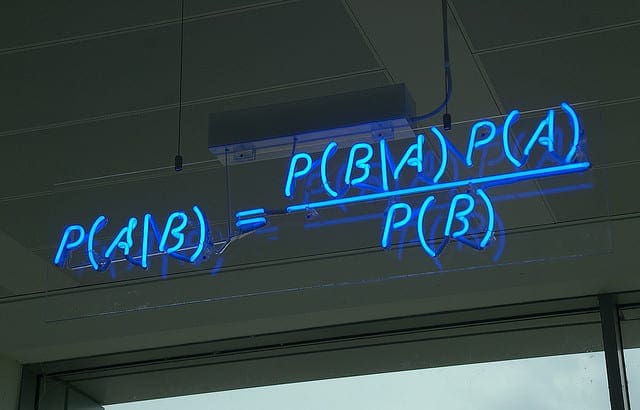
Naive Bayes được ưa chuộng nhờ vào sự đơn giản trong cài đặt, tốc độ nhanh chóng khi xử lý dữ liệu lớn, và khả năng mở rộng cho nhiều loại dữ liệu khác nhau. Trong bài viết này, chúng ta sẽ đi sâu vào phần toán học phía sau Naive Bayes, các biến thể phổ biến của nó, và phân tích ưu và nhược điểm của phương pháp này.

2. Naive Bayes Classifier - Phần toán

2.1. Định lý Bayes

Naive Bayes Classifier dựa trên định lý Bayes, công thức tổng quát như sau:

\[P(C \mid X) = \frac{P(X \mid C) \cdot P(C)}{P(X)}\]

Thuật toán Naive Bayes tính xác suất của từng class cho một mẫu dữ liệu mới, và chọn class có xác suất cao nhất làm kết quả phân loại. Điểm quan trọng là giả định Naive Bayes đưa ra: các đặc trưng $X_i$ là độc lập có điều kiện dựa trên class $C$. Điều này cho phép công thức được viết lại dưới dạng:

\[P(C \mid X_1, X_2, ..., X_n) \propto P(C) \cdot \prod_{i=1}^{n} P(X_i \mid C)\]

2.2. Gaussian Naive Bayes

Gaussian Naive Bayes (GNB) được sử dụng khi các feature là số và giả định rằng các đặc trưng này tuân theo phân phối Gauss. Với GNB, xác suất $P(X_i \mid C)$ được tính bằng hàm mật độ xác suất của phân phối Gaussian:

\[P(X_i \mid C) = \frac{1}{\sqrt{2\pi \sigma_{iC}^2}}exp(-\frac{(X_i - \mu_{iC})^2}{2\sigma_{iC}^2})\]

Trong đó, $\mu_{iC}$ và $\sigma_{iC}^2$ là trung bình và phương sai của phân phối Gauss của feature đó trong class $C$.

2.3. Multinomial Naive Bayes

Multinomial Naive Bayes (MNB) chủ yếu được sử dụng cho các bài toán phân loại văn bản, nơi dữ liệu được biểu diễn dưới dạng tần suất hoặc xác suất xuất hiện của các từ (hoặc đặc trưng) trong một tài liệu. Với MNB, xác suất $P(X_i \mid C)$ được tính dựa trên tần suất xuất hiện của từ $X_i$ trong các tài liệu thuộc class $C$:

\[P(X_i \mid C) = \frac{N_{iC} + \alpha}{N_C + \alpha \vert V \vert}\]

Trong đó,

* $N_{iC}$ : tổng số lần xuất hiện của $X_i$ trong các tài liệu thuộc class $C$

* $N_C$: tổng số từ trong các tài liệu ở class $C$

* $\vert V \vert$: kích thước từ vựng

* $\alpha$: giá trị làm mượt để tránh bị probability = 0, thường sử dụng Laplace smoothing với $\alpha = 1.$

2.4. Complement multinomial Naive Bayes

Complement Naive Bayes (CNB) là một biến thể của MNB, đặc biệt hữu ích cho các tập dữ liệu mất cân bằng. Thay vì tính xác suất $P(X_i \mid C)$ trực tiếp cho một class, CNB tính xác suất của từ $X_i$ trong tất cả các class khác ngoài class $C$. Điều này giúp CNB hoạt động tốt hơn khi có sự chênh lệch lớn giữa các class.

Công thức của CNB:

\[P(X_i \mid C) = \frac{N_{i \overline{C}} + \alpha}{N_{\overline{C}} + \alpha|V|}\]

Trong đó,

* $N_{i \overline{C}}$: tổng số lần xuất hiện của $X_i$ trong các tài liệu không thuộc class $C$.

* $N_{\overline{C}}$: tổng số từ trong các tài liệu không thuộc class $C$.

* $\vert V \vert$: kích thước từ vựng.

* $\alpha$: giá trị làm mượt để tránh bị probability = 0, thường sử dụng Laplace smoothing với $\alpha = 1.$.

3. Ưu và nhược

Ưu điểm

Đơn giản và dễ triển khai
Không yêu cầu nhiều dữ liệu huấn luyện
Xử lý tốt cả dữ liệu số (numerical) và
Thời gian xử lý nhanh
Ít bị ảnh hưởng bởi các feature không liên quan (curse of dimensionality)

Nhược điểm

Naive Bayes giả định rằng tất cả các đặc trưng (hoặc yếu tố dự báo) là độc lập, điều này hiếm khi xảy ra trong thực tế. Điều này giới hạn tính ứng dụng của thuật toán trong các trường hợp thực tế.
Các ước lượng của nó có thể không chính xác trong một số trường hợp, vì vậy không nên quá tin tưởng và dùng vào các giá trị xác suất mà nó trả về để tham dự các cuộc thi hoặc viết papers.

4. Kết luận

Naive Bayes là một thuật toán đơn giản nhưng mạnh mẽ, đặc biệt hiệu quả với các bài toán phân loại văn bản và dữ liệu lớn. Tuy có những hạn chế về giả định độc lập và nhạy cảm với dữ liệu hiếm, các biến thể như Complement Naive Bayes có thể khắc phục phần nào những nhược điểm này, giúp mô hình phù hợp hơn cho các bài toán phức tạp và dữ liệu mất cân bằng.

References

1. 1.9. Naive Bayes - Scikit learn
2. Complement naive bayes - Cross Validated
3. Naïve Bayes Algorithm’s Advantages and Disadvantages - Kaggle