Xin chào các bạn,
Trong bài post này, mình sẽ trình bày về một giải thuật dùng để giảm chiều dữ liệu có tên là Principle Component Analysis (PCA). Đây là một giải thuật khá cổ tuy nhiên những giá trị toán học nó mang lại vẫn trường tồn theo thời gian. Chúng ta hãy cùng khám phá xem nó hoạt động như thế nào nhé.
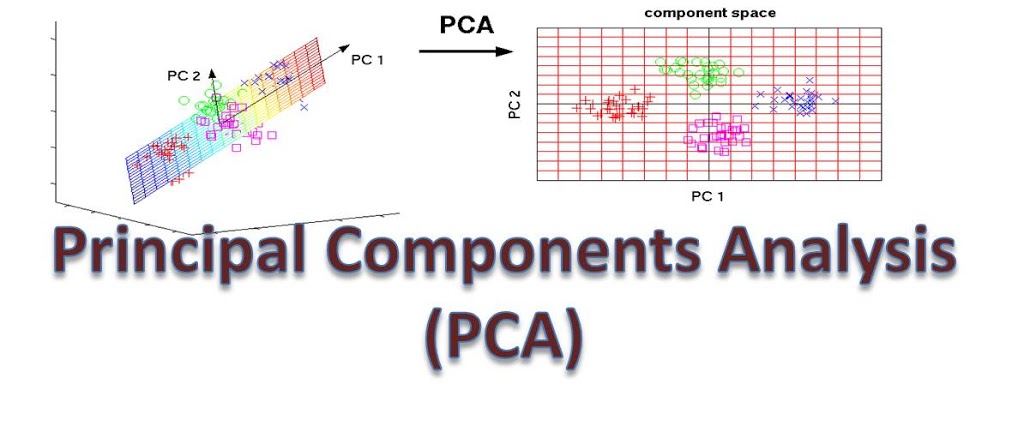
1. Giới thiệu
Như đã đề cập ở tiêu đề, PCA là một giải thuật dùng để giảm chiều của dữ liệu trong khi tối thiểu thông tin mất mát. Nó có rất nhiều ứng dụng thực tế như:
- Visualise data
- Data Compression
*
2. How it works
Ở phần này, mình sẽ hướng dẫn implement PCA với chỉ thư viện numpy. Bộ dữ liệu minh sẽ sử dụng là tập Iris dataset từ thư viện sklearn.
- Bước 1: Load các thư viện cần sử dụng
```python
import numpy as np # For calculation
from sklearn import datasets # For dataset
import matplotlib.pyplot as plt # For visualisation
%matplotlib inline
```python
data = datasets.load_iris()["data"]
print(f"Data dimension: {data.shape}")
Tập Iris dataset có dimension là 4, chúng ta muốn giảm nó xuống 2 hoặc 3 để có thể visualise nó. Và chúng ta sẽ thực hiện visualise bằng PCA.
Trước khi áp dụng PCA, data phải cần được tiêu chuẩn hóa cho các feature. Điều này giúp cho tất cả các feature của ma trận covariance có cùng 1 range với nhau.
data = data - data.mean(axis=0, keepdims=True)
- Bước 2: Tìm eigen values và eigen vectors
Ở bước 2 này, chúng ta sẽ tìm tất cả eigen values và eigen vectors của ma trận covariance data.
data_cov = np.cov(data.T)
eigen_values, eigen_vectors = np.linalg.eig(data_cov)
eigen_vectors = eigen_vectors.T
- Bước 3: Lọc ra k eigenvectors có eigenvalues lớn nhất
pca_dim = 2
assert pca_dim < data.shape[-1], "pca dim > num feature, invalid operation"
idxes = np.argsort(eigen_values)[::-1]
chosen_eigen_vectors = eigen_vectors[idxes[:pca_dim]].T
- Bước 4: Dùng k eigenvectors để làm principal components
new_data = data.dot(chosen_eigen_vectors)
print(f"Old data shape: {data.shape}, New data shape: {new_data.shape}")
Old data shape: (150, 4), New data shape: (150, 2)
Và đây là class được tích hợp từ các steps trên để thực hiện PCA cho dữ liệu.
def pca(data: np.ndarray,
pca_dim: int):
# Step 1: Rescale data
data = data - data.mean(axis=0)
data_cov = np.cov(data.T)
eigen_values, eigen_vectors = np.linalg.eig(data_cov)
eigen_vectors = eigen_vectors.T
idxes = np.argsort(eigen_values)[::-1]
chosen_eigen_vectors = eigen_vectors[idxes][:pca_dim].T
new_data = data.dot(chosen_eigen_vectors)
print(f"Old data shape: {data.shape}, New data shape: {new_data.shape}")
return new_data
Đối với giảm chiều dữ liệu, chúng ta cũng có thể cắt bỏ các chiều dữ liệu khác một cách ngẫu nhiên, tuy nhiên PCA cho chúng ta một dữ liệu với ít chiều hơn nhưng lượng thông tin giữ lại được có nhiều ý nghĩa hơn so với việc bỏ những dimension khác một cách ngẫu nhiên. Và trong nhiều trường hợp, bạn sẽ thấy việc dùng PCA còn giúp tăng đáng kể performance của ML models vì PCA giúp loại ra được những chiều thông tin dư.
Ở đây, mình sẽ thực nghiệm với tập dataset iris của sklearn để xem performance của machine learning khi được train trên PCA.
# Step 1: Import necessary libraries
from sklearn import datasets
from sklearn import tree
# Divide into train and val dataset
iris = datasets.load_iris()["data"]
X = datasets.load_iris().data
Y = datasets.load_iris().target
idxes = np.random.permutation(len(X))
X_train = X[idxes[:100]]
Y_train = Y[idxes[:100]]
X_val = X[idxes[100:]]
Y_val = Y[idxes[100:]]
print(f"X_train shape: {X_train.shape}, Y_train shape: {Y_train.shape}, X_val shape: {X_val.shape}, Y_val shape: {Y_val.shape}")
# Perform PCA on X_train dataset
pca = PCA(2)
pca.fit(X_train)
X_train_transformed = pca.transform(X_train)
X_val_transformed = pca.transform(X_val)
# Init classifiers
classifier1 = tree.DecisionTreeClassifier()
classifier1 = classifier1.fit(X_train, Y_train)
classifier2 = tree.DecisionTreeClassifier()
classifier2 = classifier2.fit(X_train_transformed, Y_train)
# Inference on val set
non_pca_predictions = classifier1.predict(X_val)
pca_predictions = classifier2.predict(X_val_transformed)
print(f"Without PCA Accuracy: {len(non_pca_predictions[non_pca_predictions==Y_val])/len(non_pca_predictions)}")
print(f"With PCA Accuracy: {len(pca_predictions[pca_predictions==Y_val])/len(pca_predictions)}")
Without PCA Accuracy: 0.96
With PCA Accuracy: 1.0
Ở ví dụ này, PCA đã giúp chúng ta tăng accuracy lên 100%. Ở case này, PCA giúp chúng ta cô đọng được thông tin nhiều hơn và có thể đã giảm được hiện tượng overfitting trên tập train nên đã dẫn tới kết quả tốt hơn.
3. Giải thích toán của PCA
Principal Component Analysis là lời giải cho bài toán optimisation ứng dụng phương pháp Larange. Ta có phát biểu của bài toán như sau: