Xin chào các bạn,
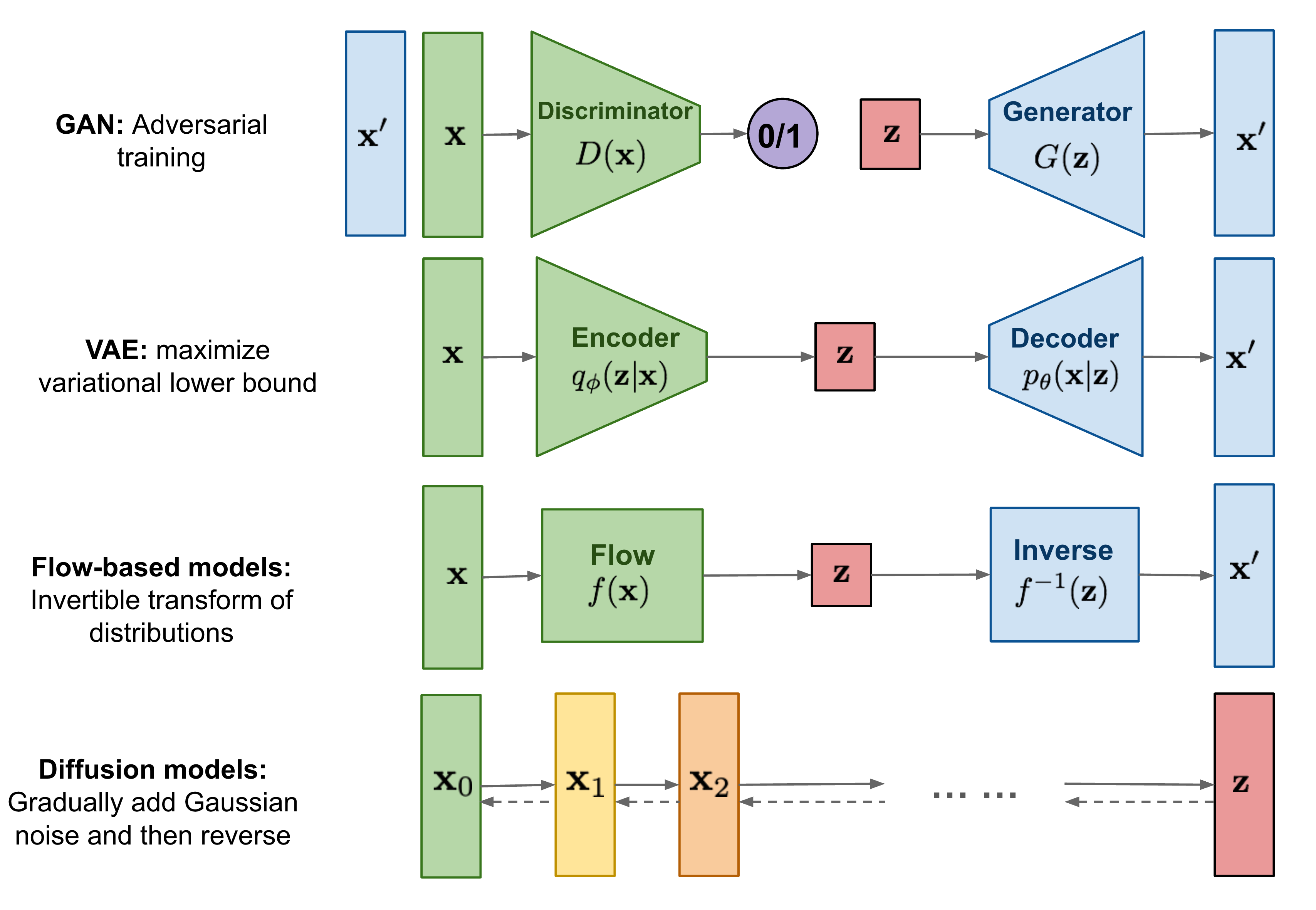
Cho đến nay, mình đã viết về hai loại mô hình sinh dữ liệu, gồm GANs và VAE. Chúng đã cho thấy thành công lớn trong việc tạo ra các hình ảnh có chất lượng rất tốt, nhưng mỗi loại đều có những hạn chế riêng. Mô hình GAN thường gặp phải vấn đề bất ổn trong quá trình training và thiếu đa dạng trong quá trình sinh dữ liệu do bản chất adversarial learning của nó. VAE dựa vào một hàm loss xấp xỉ (surrogate loss).
Mô hình Diffusion được lấy cảm hứng từ nhiệt động học phi cân bằng (Non-equilibrium thermodynamics). Chúng áp dụng Markov chain của các bước khuếch tán nhằm dần dần thêm random noise vào data, sau đó học cách đảo ngược quá trình khuếch tán để tạo ra các mẫu dữ liệu mong muốn từ nhiễu. Không giống như GANs và VAE, mô hình Diffusion được huấn luyện theo một quy trình cố định và latent dimension có dimension bằng với data.
1. Mô hình Diffusion là gì và nó hoạt động như thế nào ?
Stable Diffusion là một loại mô hình tạo sinh dựa trên quá trình khuếch tán, hoạt động thông qua hai bước chính: forward process và reverse process.
Trong lúc training, diffusion được chia thành 2 quá trình:
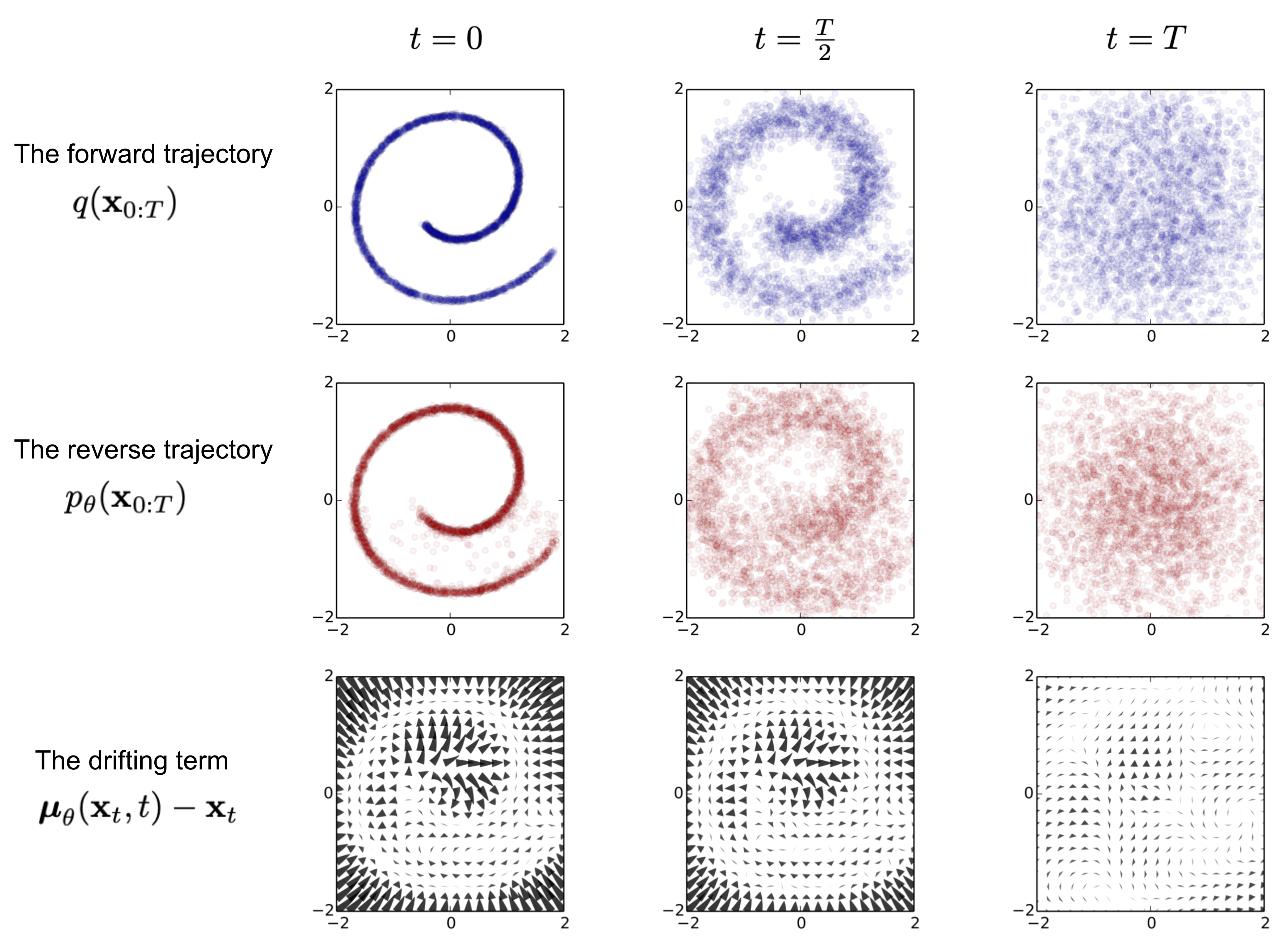
- Forward process: Dữ liệu gốc, như hình ảnh, dần bị thêm nhiễu qua nhiều bước. Mỗi bước làm cho dữ liệu trở nên ngày càng ngẫu nhiên hơn, đến khi đạt trạng thái gần giống như nhiễu thuần túy. Quá trình này được thực hiện theo chuỗi Markov, và mô hình không học trong giai đoạn này.

- Reverse process: Mô hình học cách đảo ngược quá trình nhiễu, tái tạo lại dữ liệu gốc từ nhiễu. Thông qua mạng neural networks, mô hình predict các bước khử nhiễu ngược lại từng bước một, từ nhiễu ngẫu nhiên trở về dạng dữ liệu có cấu trúc, như hình ảnh rõ ràng.

Trong lúc inference, ta chỉ sử dụng reverse process bằng việc đưa vào nhiễu Gauss và mô hình sẽ trả kết quả là một tấm ảnh bất kì được sinh ra.
2. Giải thích toán học
2.1. Forward process
Với một điểm dữ liệu được lấy mẫu từ phân phối dữ liệu thực \(x_0 \sim q(x)\), chúng ta tiến hành forward process bằng cách thêm một lượng nhỏ nhiễu Gaussian vào mẫu qua \(T\) bước, tạo ra một chuỗi các mẫu bị nhiễu với cường độ tăng dần. Mức độ nhiễu ta thêm vào sẽ được định nghĩa bởi một scheduler \(\{ \beta_t \in (0, 1) \}_{t=1}^T\).
\[q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \quad
q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\]
Mẫu dữ liệu \(x_0\) dần mất đi các đặc điểm nhận dạng khi timestep \(t\) lớn dần. Cuối cùng, khi \(T \rightarrow \infty\), \(x_T\) tương đương với một phân phối Gaussian đẳng hướng (isotropic Gaussian).
Một tính chất thú vị của quá trình trên là chúng ta có thể lấy mẫu \(x_t\) tại bất kỳ bước time step \(t\) nào bằng cách sử dụng reparameterisation trick. Đặt \(\alpha_t = 1 - \beta_t\), và \(\bar{\alpha}_t = \prod^t_{i=1} \alpha_i\).
\[\begin{aligned}
\mathbf{x}_t
&= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} & \text{ ;Với } \boldsymbol{\epsilon}_{t-1}, \boldsymbol{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\
&= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} & \text{ ;với } \bar{\boldsymbol{\epsilon}}_{t-2} \text{ là hợp của 2 phân phối Gauss (*).} \\
&= \dots \\
&= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon} \\
q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I})
\end{aligned}\]
(*) Khi chúng ta gộp hai phân phối Gaussian với phương sai khác nhau \(\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})\) và \(\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})\) phân phối mới sẽ là \(\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})\). Ở đây, độ lệch chuẩn sau khi gộp là \(\sqrt{(1 - \alpha_t) + \alpha_t (1-\alpha_{t-1})} = \sqrt{1 - \alpha_t\alpha_{t-1}}\).
2.2. Reverse process
Nếu chúng ta có thể đảo ngược quá trình trên và lấy mẫu từ \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\), chúng ta sẽ có thể tái tạo mẫu thực từ đầu vào nhiễu Gaussian, \(\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\). Lưu ý rằng nếu \(\beta_t\) đủ nhỏ, \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\) cũng sẽ là Gaussian. Tuy nhiên, chúng ta không thể dễ dàng ước lượng \(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t)\) vì nó cần tính prior \(q(x_t)\) và việc này intractable, do đó chúng ta cần học một mô hình \(p_\theta\) để xấp xỉ các xác suất có điều kiện này nhằm thực hiện quá trình reverse mà không cần phải tính prior.
\[p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad
p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\]
Tuy nhiên, khi chỉ condition trên timestep \(t-1\) sẽ có thể có rất nhiều uncertainty vì từ một bưc ảnh đầy nhiễu hoặc mờ mờ nhiễu, chúng ta sẽ có thể có rất nhiều kết quả tạo sinh không mong muốn. Và nếu có thể condition trên cả \(x_0\) thì điều này sẽ làm giảm đáng kể uncertainty. Tuy nhiên, khi condition với \(x_0\) thì công thức toán sẽ phức tạp hơn nhưng trong trường hợp này thì bài toán của chúng ta vẫn có thể giải được. Cụ thể, tác giả diễn giải như sau:
\[q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\beta}_t} \mathbf{I})\]
Áp dụng định lý Bayes, ta được:
\[\begin{aligned}
q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
&= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\
&\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
&= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t {\mathbf{x}_{t-1}} {+ \alpha_t} {\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ {\mathbf{x}_{t-1}^2} {- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} {\mathbf{x}_{t-1}} {+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
&= \exp\Big( -\frac{1}{2} \big( {(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - {(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} { + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)}
\end{aligned}\]
Trong đó \(C(\mathbf{x}_t, \mathbf{x}_0)\) là một hàm không liên quan đến \(\mathbf{x}_{t-1}\) và bị lược bỏ. Theo hàm mật độ của phân phối Gaussian chuẩn, giá trị trung bình và phương sai có thể được tham số hóa như sau (nhớ rằng \(\alpha_t = 1 - \beta_t\) và \(\bar{\alpha}_t = \prod_{i=1}^T \alpha_i\)):
\[\begin{aligned}
\tilde{\beta}_t
&= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})
= 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})})
= {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\
\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0)
&= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\
&= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\
&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\
\end{aligned}\]
Nhờ vào tính chất thú vị này, chúng ta có thể biểu diễn \(\mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t)\) và thay vào phương trình trên để thu được:
\[\begin{aligned}
\tilde{\boldsymbol{\mu}}_t
&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\
&= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)}
\end{aligned}\]
2.3. Loss function
Hàm loss của stable diffusion khá ngắn gọn, \(- \log p_\theta(\mathbf{x}_0)\). Với hàm loss này, ta phải train một mô hình theo giải thuật như trên (forward-reverse process) và tạo ra được data mà có log-likelihood với lại tập training data cao. Nói cách khác, nếu ảnh được sinh ra có phân phối giống với training data thì hàm loss kia sẽ thấp và ngược lại.
Biến đổi một chút, ta sẽ có được cách tính của hàm loss trên:
\[p_\theta(x_0) = \int p_\theta(x_{0:T}) dx_{1:T}\]
Để tính được hàm loss, chúng ta phải tính tích phân trên tất cả các time step \(x_1, x_2, ..., x_{T-1}, x_{T-2}\). Và việc tính này sẽ càng trở nên intractable nếu ảnh được gen ra có độ phân giải lớn và số lượng timesteps nhiều.
Với cách dùng Evidence Lower Bound và biến đổi, chúng ta sẽ không cần phải tính tích phân trên một miền rộng lớn như vậy và việc này biến bài toán trở nên tractable (thú vị không nào ^_^). Bài toán được biến đổi như sau:
\[\begin{aligned}
- \log p_\theta(\mathbf{x}_0)
&\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) \\
&= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\
&= -\log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\
&= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\
\text{Let }L_\text{VLB}
&= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0)
\end{aligned}\]
\[\begin{aligned}
L_\text{VLB}
&= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\
&= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\
&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\
&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\
&= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\
&= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\
&= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ]
\end{aligned}\]
\[\begin{aligned}
L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\
\text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\
L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\
L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)
\end{aligned}\]
Mỗi thành phần KL trong \(L_\text{VLB}\) (ngoại trừ \(L_0\)) so sánh hai phân phối Gaussian và do đó chúng có thể được tính toán dưới dạng closed-form. \(L_T\) là hằng số và có thể bị bỏ qua trong quá trình huấn luyện vì \(q\) không có tham số có thể học được và là một nhiễu Gaussian.
Hãy nhớ rằng chúng ta cần học một mạng neural để xấp xỉ các phân phối xác suất có điều kiện trong reverse process, \(p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\). Chúng ta muốn huấn luyện \(\boldsymbol{\mu}_\theta\) để dự đoán \(\tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)\). Vì \(\mathbf{x}_t\) có sẵn như đầu vào trong thời gian huấn luyện, chúng ta có thể tái tham số hóa thành phần nhiễu Gaussian thay vào đó để nó dự đoán \(\boldsymbol{\epsilon}_t\) từ đầu vào \(\mathbf{x}_t\) tại timestep \(t\):
\[\begin{aligned}
\boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\
\text{Thus }\mathbf{x}_{t-1} &= \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))
\end{aligned}\]
Hàm loss \(L_t\) được tham số hóa để minimise sự khác biệt từ \(\tilde{\boldsymbol{\mu}}\) bằng cách sử dụng L2 loss và hệ số \(\frac{1}{2 \sigma ^2}\) cho việc scaling. Các bạn cũng có thể sử dụng nhiều loại khác như L1 loss, Huber loss, Entropy loss, … Phổ biến nhất vẫn dùng là L2 loss.
\[\begin{aligned}
L_t
&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| {\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\
&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \| {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \|^2 \Big] \\
&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\
&= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big]
\end{aligned}\]
Thực nghiệm cho thấy việc huấn luyện mô hình diffusion hoạt động hiệu quả hơn với việc lược đi trọng số:
\[\begin{aligned}
L_t^\text{simple}
&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\
&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big]
\end{aligned}\]
Lưu ý rằng hàm loss cuối cùng này đã bao gồm cả \(L_0\) ở trên. Do về mặt bản chất, \(L_0\) cũng là đo khoảng cách KL giữa training data ban đầu và data được sinh với đầu vào là \(x_1\).
3. Implementation
- Step 1: Import các thư viện cần thiết
import torch
import torchvision
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch import nn
import math
from torchvision import transforms
from torch.utils.data import DataLoader
import numpy as np
from torch.optim import Adam
from tqdm import tqdm
- Step 1: Download dataset và tạo dataloader
IMG_SIZE = 28
BATCH_SIZE = 128
def load_transformed_dataset():
data_transforms = [
transforms.Resize((IMG_SIZE, IMG_SIZE)),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(), # Scales data into [0,1]
transforms.Lambda(lambda t: (t * 2) - 1) # Scale between [-1, 1]
]
data_transform = transforms.Compose(data_transforms)
train = torchvision.datasets.MNIST(root=".", download=True,
transform=data_transform, train=True)
test = torchvision.datasets.MNIST(root=".", download=True,
transform=data_transform, train=False)
return torch.utils.data.ConcatDataset([train, test])
data = load_transformed_dataset()
dataloader = DataLoader(data, batch_size=BATCH_SIZE, shuffle=True, drop_last=True)
- Step 3: Các functions hỗ trợ cho stable diffusion
def linear_beta_schedule(timesteps: float, start: float = 0.0001, end: float = 0.02):
return torch.linspace(start, end, timesteps)
def get_index_from_list(vals, t, x_shape):
"""
Returns a specific index t of a passed list of values vals
while considering the batch dimension.
"""
batch_size = t.shape[0]
out = vals.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
Bước forward của stable diffusion sẽ được implement theo công thức:
\[\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}\]
def forward_diffusion_sample(x_0: torch.Tensor, t: torch.Tensor, device="cpu"):
"""
Closed-form forward diffusion step processed in batches.
"""
noise = torch.randn_like(x_0)
sqrt_alphas_cumprod_t = get_index_from_list(sqrt_alphas_cumprod, t, x_0.shape)
sqrt_one_minus_alphas_cumprod_t = get_index_from_list(
sqrt_one_minus_alphas_cumprod, t, x_0.shape
)
# mean + variance
return sqrt_alphas_cumprod_t.to(device) * x_0.to(device) \
+ sqrt_one_minus_alphas_cumprod_t.to(device) * noise.to(device), noise.to(device)
class Block(nn.Module):
def __init__(self, in_ch, out_ch, time_emb_dim, up=False):
super().__init__()
self.time_mlp = nn.Linear(time_emb_dim, out_ch)
if up:
self.conv1 = nn.Conv2d(in_ch + out_ch, out_ch, 3, padding=1) # Supports skip connection
self.transform = nn.ConvTranspose2d(out_ch, out_ch, 4, 2, 1)
else:
self.conv1 = nn.Conv2d(in_ch, out_ch, 3, padding=1)
self.transform = nn.Conv2d(out_ch, out_ch, 4, 2, 1)
self.conv2 = nn.Conv2d(out_ch, out_ch, 3, padding=1)
self.bnorm1 = nn.BatchNorm2d(out_ch)
self.bnorm2 = nn.BatchNorm2d(out_ch)
self.relu = nn.ReLU(inplace=True)
def forward(self, x, t, skip=None):
# First Conv + Time embedding
h = self.bnorm1(self.relu(self.conv1(x)))
time_emb = self.relu(self.time_mlp(t))
time_emb = time_emb[(...,) + (None,) * 2]
h = h + time_emb
# Skip connection if provided
if skip is not None:
h = torch.cat((h, skip), dim=1)
# Second Conv
h = self.bnorm2(self.relu(self.conv2(h)))
# Down or Upsample
return self.transform(h)
class SinusoidalPositionEmbeddings(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, time):
device = time.device
half_dim = self.dim // 2
embeddings = math.log(1e4) / (half_dim - 1)
embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
embeddings = time[:, None] * embeddings[None, :]
embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
return embeddings
class Block(nn.Module):
def __init__(self, in_ch, out_ch, time_emb_dim, up=False):
super().__init__()
self.time_mlp = nn.Linear(time_emb_dim, out_ch)
self.up = up
if up:
self.conv1 = nn.Conv2d(in_ch, out_ch, 3, padding=1)
self.transform = nn.ConvTranspose2d(out_ch, out_ch, 4, 2, 1)
else:
self.conv1 = nn.Conv2d(in_ch, out_ch, 3, padding=1)
self.transform = nn.Conv2d(out_ch, out_ch, 4, 2, 1)
self.conv2 = nn.Conv2d(out_ch, out_ch, 3, padding=1)
self.bnorm1 = nn.BatchNorm2d(out_ch)
self.bnorm2 = nn.BatchNorm2d(out_ch)
self.relu = nn.ReLU(inplace=True)
def forward(self, x, t):
# First Conv
h = self.bnorm1(self.relu(self.conv1(x)))
# Add time embedding
time_emb = self.relu(self.time_mlp(t))
time_emb = time_emb[(..., ) + (None, ) * 2]
h = h + time_emb
# Second Conv
h = self.bnorm2(self.relu(self.conv2(h)))
# Add skip connection
if h.shape == x.shape:
h = h + x
# Transform
return self.transform(h)
class SimpleUnet(nn.Module):
"""
A simplified variant of the U-Net architecture with ResNet-style skip connections.
"""
def __init__(self):
super().__init__()
image_channels = 1
down_channels = (32, 64, 128)
up_channels = (128, 64, 32)
out_dim = 1
time_emb_dim = 32
# Time embedding
self.time_mlp = nn.Sequential(
SinusoidalPositionEmbeddings(time_emb_dim),
nn.Linear(time_emb_dim, time_emb_dim),
nn.ReLU(inplace=True)
)
# Initial projection
self.conv0 = nn.Conv2d(image_channels, down_channels[0], 3, padding=1)
# Downsample blocks
self.downs = nn.ModuleList([
Block(down_channels[i], down_channels[i+1], time_emb_dim)
for i in range(len(down_channels) - 1)
])
# Upsample blocks
self.ups = nn.ModuleList([
Block(up_channels[i], up_channels[i+1], time_emb_dim, up=True)
for i in range(len(up_channels) - 1)
])
# Final output layer
self.output = nn.Conv2d(up_channels[-1], out_dim, 1)
def forward(self, x, timestep):
# Embed time
t = self.time_mlp(timestep)
# Initial projection
x = self.conv0(x)
# Downsampling with skip connections
skip_connections = []
for down in self.downs:
x = down(x, t)
skip_connections.append(x)
# Upsampling with ResNet-style skip connections
for up in self.ups:
skip_x = skip_connections.pop()
if x.shape == skip_x.shape: # Ensure shapes match for addition
x = x + skip_x
x = up(x, t)
# Final output
return self.output(x)
model = SimpleUnet()
print("Num params: ", sum(p.numel() for p in model.parameters()))
Mình sẽ sử dụng Huber Loss, các bạn cũng có thể các hàm loss khác mình đề xuất ở trên.
def get_loss(model, x_0, t):
x_noisy, noise = forward_diffusion_sample(x_0, t, device)
noise_pred = model(x_noisy, t)
return F.huber_loss(noise, noise_pred)
# Define beta schedule
T = 300
betas = linear_beta_schedule(timesteps=T)
# Pre-calculate different terms for closed form
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
# Training
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
optimizer = Adam(model.parameters(), lr=0.001)
epochs = 100
for epoch in range(epochs):
epoch_loss = 0
for step, batch in enumerate(tqdm(dataloader)):
optimizer.zero_grad()
t = torch.randint(0, T, (BATCH_SIZE,), device=device).long()
loss = get_loss(model, batch[0], t)
epoch_loss += loss.item()
loss.backward()
optimizer.step()
print(f"Epoch: {epoch}, Total loss: {epoch_loss}")
100%|██████████| 546/546 [00:21<00:00, 25.97it/s]
Epoch: 0, Total loss: 25.88470129109919
100%|██████████| 546/546 [00:19<00:00, 28.07it/s]
Epoch: 1, Total loss: 14.593471519649029
100%|██████████| 546/546 [00:19<00:00, 27.87it/s]
Epoch: 2, Total loss: 13.600953148677945
100%|██████████| 546/546 [00:20<00:00, 27.10it/s]
Epoch: 3, Total loss: 13.152173833921552
100%|██████████| 546/546 [00:19<00:00, 27.36it/s]
...
- Step 7: Inference and visualisation
Bước inference sẽ được thực hiện theo công thức sau:
\[\begin{aligned}
\hat{\boldsymbol{x}}_{t-1}
&= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(x_t, t) \Big)} + {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \cdot \epsilon
\end{aligned}\]
@torch.no_grad()
def sample_timestep(x, t):
"""
Calls the model to predict the noise in the image and returns
the denoised image.
Applies noise to this image, if we are not in the last step yet.
"""
betas_t = get_index_from_list(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = get_index_from_list(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = get_index_from_list(sqrt_recip_alphas, t, x.shape)
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
)
posterior_variance_t = get_index_from_list(posterior_variance, t, x.shape)
return model_mean + torch.sqrt(posterior_variance_t) * torch.randn_like(x)
model.eval()
fully_noised_sample = torch.randn((1, 1, 28, 28)).cuda()
generated_sample = fully_noised_sample.clone()
for timestep in tqdm(range(T-1, -1, -1)):
timestep = torch.Tensor([timestep]).long().cuda()
generated_sample = sample_timestep(generated_sample, timestep)
plt.imshow(generated_sample[0, 0].detach().cpu())
4. Kết luận
Diffusion model là một mô hình sinh dữ liệu dựa trên 2 quá trình tuần tự là forward process và reverse process. Khác với các mô hình sinh dùng adversarial training như GAN hay surrogate loss như VAE, diffusion model thực hiện quá trình thêm nhiễu dần dần vào dữ liệu, sau đó học cách đảo ngược quá trình để tái tạo lại mẫu gốc từ nhiễu. Điều này giúp mô hình có thể tuần tự và chậm rãi sinh ra kết quả, vì vậy sự ổn định cũng được cải thiện hơn nhiều so với các phương pháp trước đó. Với tiềm năng vượt trội và tính đơn giản trong kiến trúc, các mô hình diffusion đã chứng tỏ hiệu quả cao trong việc sinh data.
Trong bài viết này, mình đã giới thiệu về diffusion model, cách hoạt động, và các chi tiết toán học của nó. Hy vọng các bạn cảm thấy hữu ích. Chúc các bạn học tốt!.
P/s: Bài viết được lấy chủ yếu từ blog tuyệt vời của Lilian blog và được bổ sung thêm một vài chi tiết toán để giúp các công thức toán nhẹ nhàng hơn so với bài viết gốc. Vì vậy, xin chân thành cảm ơn Lilian Weng.
References
1. What are Diffusion Models? - Lil’s blog
2. Diffusion Models | Paper Explanation | Math Explained