Giải thích và code Variational AutoEncoder

May 18, 2024

Xin chào các bạn!

Trong bài post này, mình sẽ giới thiệu về mô hình Variational AutoEncoder được công bố trong paper “Auto-Encoding Variational Bayes” của tác giả Diederik P. Kingma và các cộng sự. Đây là một kiến trúc tương tự như AutoEncoder và có thêm thành phần stochastic trong phần bottleneck để khiến cho nó có khả năng tạo ra những data mới lạ (tuy vẫn thuộc distribution của training dataset).

1. Tổng quan

Được chính thức published trong paper “Auto-Encoding Variational Bayes” vào năm 2014, Variational AutoEncoder đã tạo ra tiếng vang rất lớn và tạo ra một cú hích giúp ngày càng nhiều probabilistic models được nghiên cứu hơn. Trong paper của mình, tác giả đề cập tới kiến trúc tổng quan của mô hình, các công thức toán học chứng minh, và một vài tricks để làm cho VAE có thể hoạt động được. Mình nói tricks để giúp cho model hoạt động được bởi nếu không có trick này thì chắc chắn VAE sẽ không work và các probabilistic models sau này cũng sẽ không phát triển mạnh như bây giờ.

Về cơ bản, VAE được dùng để tạo ra các dữ liệu mới từ tập data training. Ngoài ra, mô hình còn giải quyết điểm yếu cố hữu của mô hình Auto-Encoder truyền thống trong việc generate data. Một chút về nhược điểm về Auto-Encoder, mô hình này bị ván đề không sinh ra được data đa dạng và không có tính liên tục trong latent space. Với sự ra mắt của VAE, 2 nhược điểm này đã được khắc phục.

Hình 1.1. Ảnh được sinh ra từ VAE

2. Kiến trúc

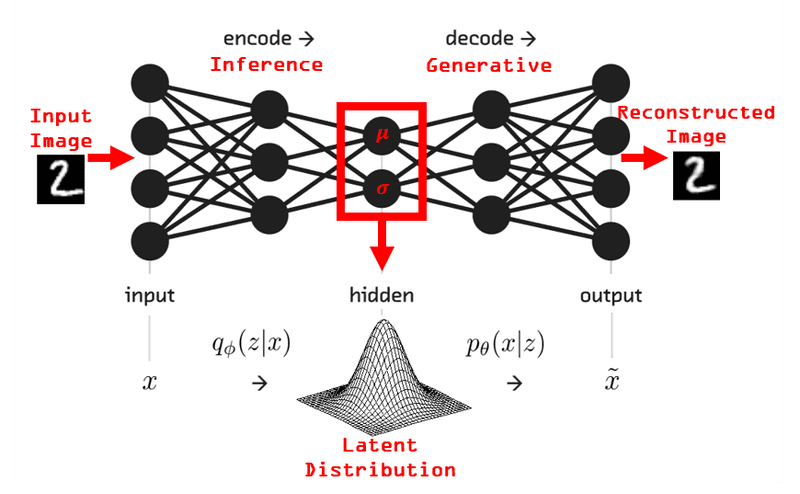Hình 2.1. Kiến trúc tổng quan của VAE

Về cơ bản, kiến trúc VAE giống gần như 99% với Auto-Encoder. VAE cũng bao gồm encoder, bottleneck, decoder, tuy nhiên có một sự khác biệt ở bottleneck. Đó là ở bottleneck của VAE, nó sẽ có 2 output là mean và standard deviation thay vì chỉ có một output bottleneck như Auto-Encoder. Tuy nhiên, 2 khối này sẽ được kết hợp lại bằng các element-wise operations để đưa vào decoder block tương tự như auto-encoder.

3. Giải thích toán học

VAE bao gồm 2 khối: Encoder, và Decoder. Khối encoder có nhiệm vụ nén và mã hóa thông tin trong khi khối decoder có nhiệm vụ khôi phục lại thông tin từ thông tin từ encoder. Việc này có thể được mô tả bằng toán học như sau:

\[\text{Encoder: } p(z|x) = \frac{p(x|z)p(z)}{p(x)}\] \[\text{Decoder: } p(x|z) = \frac{p(z|x)p(x)}{p(z)}\]

Đáng tiếc, 2 công thức trên đều rất khó để tính toán vì các priors.

Cụ thể,

\[p(x) = \int p(x|z)p(z)dz\] \[p(z) = \int p(z|x)p(x)dx\]

Nhìn vào 2 công thức trên, chúng ta có quan sát như sau. Để tính đươc p(x), ta phải quét qua toàn bộ các giá trị của latent space và để tính được p(z) ta phải quét qua toàn bộ các giá trị của data x. Nếu latent space và dataset của chúng ta > 1-D, điều này có thể khả thi, tuy nhiên chúng ta thường encode nó trong không gian lớn hơn rất nhiều so với 1D, vậy cần phải có cách khác.

Cách mà tác giả đề xuất trong paper là dùng một hàm xấp xỉ (approximator) để tính các giá trị latent (z) và reconstructed data (\(\hat{x}\)). Cụ thể, chúng sẽ có biểu thức toán học như sau:

\[\text{Encoder: } p(z|x) = \frac{p(x|z)p(z)}{p(x)} \text{ (intractable)} => q_{\theta}(z|x)\] \[\text{Decoder: } p(x|z) = \frac{p(z|x)p(x)}{p(z)} \text{ (intractable)} => q_{\phi}(x|z)\]

Trong công thức tính của Encoder đã bao gồm Decoder và ngược lại, vì vậy chúng ta chỉ cần tối ưu một trong hai khối và khối còn lại sẽ tự động được tối ưu. Trong paper của tác giả, họ chọn tối ưu Encoder nên trong post này mình cũng sẽ sử dụng Encoder để align với tác giả.

Vì chúng ta muốn hàm Encoder \(q_{\theta}(z|x)\) xấp xỉ giống y hệt như hàm intractable \(p(z|x)\) nên ta sẽ có hàm mục tiêu như sau:

\[\underset{\theta, \phi}{\text{Minimise }} D_{KL}(q_{\theta}(z|x)||p(z|x)) \text{ (1)}\] \[\underset{\theta, \phi}{\text{Minimise }} \mathbb{E}_{q_{\theta}(z|x)}[log(\frac{q_{\theta}(z|x)}{p(z|x)})] \text{ (2)}\] \[\underset{\theta, \phi}{\text{Minimise }} \mathbb{E}_{q_{\theta}(z|x)}[log(q_{\theta}(z|x)) - log(p(x, z))] + log(p(x)) \text{ (3)}\]

\(p(x)\) có thể bị lược ra khỏi hàm loss vì nó không có params tối ưu và không có công dụng nào. Tuy nhiên, ở phần dưới sẽ có một trường hợp không có params tối ưu nhưng vẫn được giữ lại.

\[\underset{\theta, \phi}{\text{Minimise }} \mathbb{E}_{q_{\theta}(z|x)}[log(q_{\theta}(z|x)) - log(p_{\phi}(x|z)) - log(p(z))] \text{ (4)}\] \[\underset{\theta, \phi}{\text{Minimise }}\mathbb{E}_{q_{\theta}(z|x)}[log(\frac{q_{\theta}(z|x)}{p(z)}) - log(p_{\phi}(x|z))] \text{ (5)}\] \[\underset{\theta, \phi}{\text{Minimise }} \mathbb{E}_{q_{\theta}(z|x)}[-log(p_{\phi}(x|z))] + D_{KL}(q_{\theta}(z|x)||p(z)) \text{ (6)}\]

Ta có gradient của phương trình trên với 2 biến \(\phi\) và \(\theta\) như sau:

\[\nabla_{\phi}\mathbb{E}_{q_{\theta}(z|x)}[-log(p_{\phi}(x|z))] + D_{KL}(q_{\theta}(z|x)||p(z)) = \nabla_{\phi}-log(p_{\phi}(x|z)) \text{ (7)}\] \[\nabla_{\theta}\mathbb{E}_{q_{\theta}(z|x)}[-log(p_{\phi}(x|z))] + D_{KL}(q_{\theta}(z|x)||p(z)) ≠ \nabla_{\theta}D_{KL}(q_{\theta}(z|x)||p(z)) \text{ (8)}\]

Ở phương trình (7), gradient có thể được tính dễ dàng nhờ vào Monte Carlo. Tuy nhiên, ở phương trình (8), ta không thể xấp xỉ bằng Monte Carlo do vướng phải parameter \(\theta\) ở phần expectation. Nếu phần phân phối tính expectation dựa vào \(\theta\) được thay bằng một biến nào đó không liên quan thì phương trình (8) sẽ đơn giản trở thành tối ưu KL divergence.

Để giải quyết vấn đề này, tác giả của paper đã đề xuất reparameterisation trick. Ý tưởng của phương pháp này như sau:

Giả sử ta có một biến \(z \sim N(\mu, \sigma^2)\), ta có thể biểu diễn nó như sau:

\[z = \mu + \sigma^2 * \epsilon\] \[\text{Với } \epsilon \sim N(\mathbf{0}, I)\]

Dựa vào reparameterisation trick, ta sẽ áp dụng như sau:

\[z = g_{\theta}(x, \epsilon) = \mu_{\theta}(x) + \sigma_{\theta}^2(x) * \epsilon\] \[\text{Với } \epsilon \sim N(\mathbf{0}, I)\]

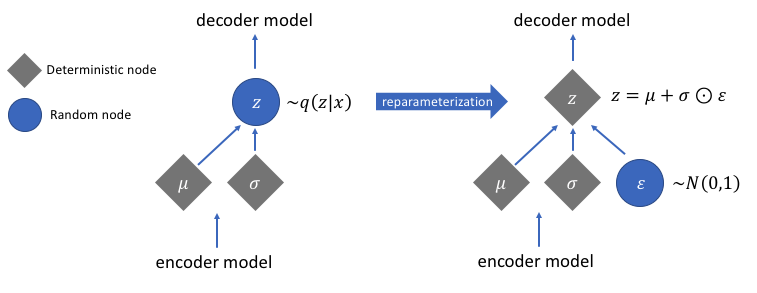Hình 3.1. Minh họa cách hoạt động của Reparameterisation trick

Áp dụng reparameterisation trick, ta biến đổi lại phương trình (8) như sau:

\[\nabla_{\theta}\mathbb{E}_{p(\epsilon)}[-log(p_{\phi}(x|z = g_{\theta}(x, \epsilon)))] + D_{KL}(q_{\theta}(z|x)||p(z)) ≠ \nabla_{\theta}D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon)|x)||p(z)) \text{ (9)}\]

Với Expectation không còn \(\theta\) trong (9), chúng ta có thể tính gradient một cách dễ dàng như sau:

\[\nabla_{\theta}\mathbb{E}_{p(\epsilon)}[-log(p_{\phi}(x|z = g_{\theta}(x, \epsilon)))] + D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) = \nabla_{\theta}D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) \text{ (10)}\]

Tới đây, chúng ta đã có được phương trình để tính gradient cập nhật trọng số cho model.

Tóm lại, chúng ta sẽ cần phương trình (7) và (10) để cập nhật các parameters trong mạng. Mình sẽ viết lại 2 phương trình sau khi được áp dụng reparameterisation trick.

\[\nabla_{\phi}\mathbb{E}_{p(\epsilon)}[-log(p_{\phi}(x|z = g_{\theta}(x, \epsilon)))] + D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) = \nabla_{\phi}-log(p_{\phi}(x|z = g_{\theta}(x, \epsilon))) \text{ (7)}\] \[\nabla_{\theta}\mathbb{E}_{p(\epsilon)}[-log(p_{\phi}(x|z = g_{\theta}(x, \epsilon)))] + D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) = \nabla_{\theta}D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) \text{ (10)}\]

Phương trình (7) chỉ đơn giản là tối ưu các tham số của decoder sao để cho reconstructed data giống với data gốc. Chúng ta có thể dùng L1, L2, Binary Cross Entropy, … Tuy nhiên, đối với phương trình (10), chúng ta phải sample từ prior \(p(z)\) và \(\epsilon \sim N(\mathbf{0}, \mathbf{I})\), và việc sample mỗi iteration mỗi khác như vậy sẽ khiến việc training khó hội tụ hơn, vì thế cần một cách thức khác để có thể tối ưu nó mà không cần sample từ các distributions.

Chúng ta sẽ assume latent space z là một phân phối Gaussian và prior của nó là một phân bố Gauss tiêu chuẩn \(p(z) = N(0, I)\) và posterior \(q_{\theta}(z = g_{\theta}(x, \epsilon)) = N(\mu_{\theta}(x), \sigma_{\theta}^2(x))\).

Vì vậy, chúng ta có thể biến đổi (10) thành:

\[\nabla_{\theta}D_{KL}(q_{\theta}(z = g_{\theta}(x, \epsilon))||p(z)) = D_{KL}(N(\mu_{\theta}(x), \sigma_{\theta}^2(x))|| N(0, I)) \text{ (11)}\]

Theo công thức Gauss, ta có:

\[q_{\theta}(z = g_{\theta}(x, \epsilon)) = \frac{1}{\sigma \sqrt {2\pi} } e^{-0.5(\frac{z - \mu_{\theta}(x)}{\sigma_{\theta}(x)})^2}\] \[p(z) = \frac{1}{\sqrt {2\pi}}e^{-0.5z^2}\]

Từ 2 công thức Gauss trên, ta áp dụng vào để tính khoảng cách Kullback-Leibler một cách deterministic.

\[D_{KL}(N(\mu_{\theta}(x), \sigma_{\theta}^2(x))|| N(0, I)) = \mathbb{E}_{q_{\theta}}[log(q_{\theta}) - log(p(z))]\] \[\mathbb{E}_{q_{\theta}}[log(\frac{1}{\sigma_{\theta} \sqrt{2 \pi}}) - \frac{1}{2}(\frac{z - \mu_{\theta}}{\sigma_{\theta}})^2 - log(\frac{1}{\sqrt{2 \pi}}) + \frac{1}{2} z^2]\] \[\mathbb{E}_{q_{\theta}}[log(\frac{1}{\sigma_{\theta} \sqrt{2 \pi}}) - log(\frac{1}{\sqrt{2 \pi}})] + \mathbb{E}_{q_{\theta}}[- \frac{1}{2}(\frac{z - \mu_{\theta}}{\sigma_{\theta}})^2] + \mathbb{E}_{q_{\theta}}[\frac{1}{2} z^2]\]

Trong đó:

\[\mathbb{E}_{q_{\theta}}[log(\frac{1}{\sigma_{\theta} \sqrt{2 \pi}}) - log(\frac{1}{\sqrt{2 \pi}})] = - \frac{1}{2}log(\sigma_{\theta})\] \[\mathbb{E}_{q_{\theta}}[- \frac{1}{2}(\frac{z - \mu_{\theta}}{\sigma_{\theta}})^2] = - \frac{1}{2}\] \[\mathbb{E}_{q_{\theta}}[\frac{1}{2} z^2] = \frac{1}{2}(\sigma_{\theta}^2 + \mu_{\theta}^2)\]

Vì vậy, tổng hợp lại ta có được là:

\[D_{KL}(N(\mu_{\theta}(x), \sigma_{\theta}^2(x))|| N(0, I)) = \frac{1}{2}[-log(\sigma_{\theta}^2) - 1 + \sigma_{\theta}^2 + \mu_{\theta}^2]\]

4. Code VAE với Python và Keras

Ở phần này, một mô hình VAE đơn giản sẽ được xây dựng và train với ngôn ngữ Python và thư viện Keras để kiểm chứng lý thuyết.

• Bước 1: Import các thư viện cần thiết

import os

os.environ["KERAS_BACKEND"] = "tensorflow"

import numpy as np
import tensorflow as tf
import keras
from keras import ops
from keras import layers
import matplotlib.pyplot as plt

• Bước 2: Model

# Sampling step from mean and var
class Sampling(layers.Layer):
    """Uses (z_mean, z_log_var) to sample z, the vector encoding a digit."""

    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.seed_generator = keras.random.SeedGenerator(1337)

    def call(self, inputs):
        z_mean, z_log_var = inputs
        batch = ops.shape(z_mean)[0]
        dim = ops.shape(z_mean)[1]
        epsilon = keras.random.normal(shape=(batch, dim), seed=self.seed_generator)
        return z_mean + ops.exp(0.5 * z_log_var) * epsilon

# Encoder
latent_dim = 2

encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(encoder_inputs)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Flatten()(x)
x = layers.Dense(16, activation="relu")(x)
z_mean = layers.Dense(latent_dim, name="z_mean")(x)
z_log_var = layers.Dense(latent_dim, name="z_log_var")(x)
z = Sampling()([z_mean, z_log_var])
encoder = keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")

# Decoder
latent_inputs = keras.Input(shape=(latent_dim,))
x = layers.Dense(7 * 7 * 64, activation="relu")(latent_inputs)
x = layers.Reshape((7, 7, 64))(x)
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(x)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2DTranspose(1, 3, activation="sigmoid", padding="same")(x)
decoder = keras.Model(latent_inputs, decoder_outputs, name="decoder")

• Bước 3: Training and loss functions

class VAE(keras.Model):
    def __init__(self, encoder, decoder, **kwargs):
        super().__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder
        self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
        self.reconstruction_loss_tracker = keras.metrics.Mean(
            name="reconstruction_loss"
        )
        self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")

    @property
    def metrics(self):
        return [
            self.total_loss_tracker,
            self.reconstruction_loss_tracker,
            self.kl_loss_tracker,
        ]

    def train_step(self, data):
        with tf.GradientTape() as tape:
            z_mean, z_log_var, z = self.encoder(data)
            reconstruction = self.decoder(z)
            reconstruction_loss = ops.mean(
                ops.sum(
                    keras.losses.binary_crossentropy(data, reconstruction),
                    axis=(1, 2),
                )
            )
            kl_loss = -0.5 * (1 + z_log_var - ops.square(z_mean) - ops.exp(z_log_var))
            kl_loss = ops.mean(ops.sum(kl_loss, axis=1))
            total_loss = reconstruction_loss + kl_loss
        grads = tape.gradient(total_loss, self.trainable_weights)
        self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
        self.total_loss_tracker.update_state(total_loss)
        self.reconstruction_loss_tracker.update_state(reconstruction_loss)
        self.kl_loss_tracker.update_state(kl_loss)
        return {
            "loss": self.total_loss_tracker.result(),
            "reconstruction_loss": self.reconstruction_loss_tracker.result(),
            "kl_loss": self.kl_loss_tracker.result(),
        }

• Bước 4: Training

(x_train, _), (x_test, _) = keras.datasets.mnist.load_data()
mnist_digits = np.concatenate([x_train, x_test], axis=0)
mnist_digits = np.expand_dims(mnist_digits, -1).astype("float32") / 255

vae = VAE(encoder, decoder)
vae.compile(optimizer=keras.optimizers.Adam())
vae.fit(mnist_digits, epochs=30, batch_size=128)

• Bước 5: Visualise kết quả

def plot_latent_space(vae, n=30, figsize=15):
    # display a n*n 2D manifold of digits
    digit_size = 28
    scale = 1.0
    figure = np.zeros((digit_size * n, digit_size * n))
    # linearly spaced coordinates corresponding to the 2D plot
    # of digit classes in the latent space
    grid_x = np.linspace(-scale, scale, n)
    grid_y = np.linspace(-scale, scale, n)[::-1]

    for i, yi in enumerate(grid_y):
        for j, xi in enumerate(grid_x):
            z_sample = np.array([[xi, yi]])
            x_decoded = vae.decoder.predict(z_sample, verbose=0)
            digit = x_decoded[0].reshape(digit_size, digit_size)
            figure[
                i * digit_size : (i + 1) * digit_size,
                j * digit_size : (j + 1) * digit_size,
            ] = digit

    plt.figure(figsize=(figsize, figsize))
    start_range = digit_size // 2
    end_range = n * digit_size + start_range
    pixel_range = np.arange(start_range, end_range, digit_size)
    sample_range_x = np.round(grid_x, 1)
    sample_range_y = np.round(grid_y, 1)
    plt.xticks(pixel_range, sample_range_x)
    plt.yticks(pixel_range, sample_range_y)
    plt.xlabel("z[0]")
    plt.ylabel("z[1]")
    plt.imshow(figure, cmap="Greys_r")
    plt.show()


plot_latent_space(vae)

Hình 4.1. Visualisation của các samples được sinh ra từ VAE

5. Kết luận

VAE là một kiến trúc tạo data với cơ chế stochastic, điều này cho khả năng tạo ra những samples khác hơn so với data gốc. Tuy nhiên, sự khác biệt này sẽ không cực kì đáng kể và chất lượng sẽ khó có thể so sánh với GAN, hoặc Diffusion models. Tuy nhiên, đây vẫn là một kiến trúc rất tốt để học học vì các kiến trúc ra sau áp dụng stochastic đa số đều dựa trên reparameterisation trick của VAE.

Trong bài, mình đã giới thiệu về VAE, các công thức toán để chứng minh VAE hoạt động, và cũng như code nó với keras và tensorflow. Hy vọng các bạn thấy hữu ích và đừng ngần ngại gửi feedback vào email mình nếu chưa hiểu hoặc thấy sai sót nhé. Chúc các bạn học tốt.

References

1. Auto-Encoding Variational Bayes - arXiv
2. Variational Autoencoder - Blog
3. Keras implementation of VAE - Keras