Xin chào các bạn,
Trong bài post này, mình sẽ giải thích về các công thức toán học Wasserstein GAN (WGAN) và code kiến trúc này from scratch với Pytorch.
1. Giới thiệu
WGAN là một kiến trúc tạo sinh (generative model) giống như GAN truyền thống với một vài sự thay đổi về hàm loss để cải thiện performance. Như các bạn đã biết, việc huấn luyện GAN truyền thống sẽ gặp rất nhiều khó khăn như collapse mode, non-convergence, diminished gradient, unbalance training, sensitive to hyperparameters, … Các bạn có thể đọc thêm bài viết của Jonathan Hui để biết thêm chi tiết về các nhược điểm của GANs truyền thống, trong post của tác giả có liệt kê đầy đủ và giải thích chi tiết các nhược điểm cố hữu của GANs truyền thống.
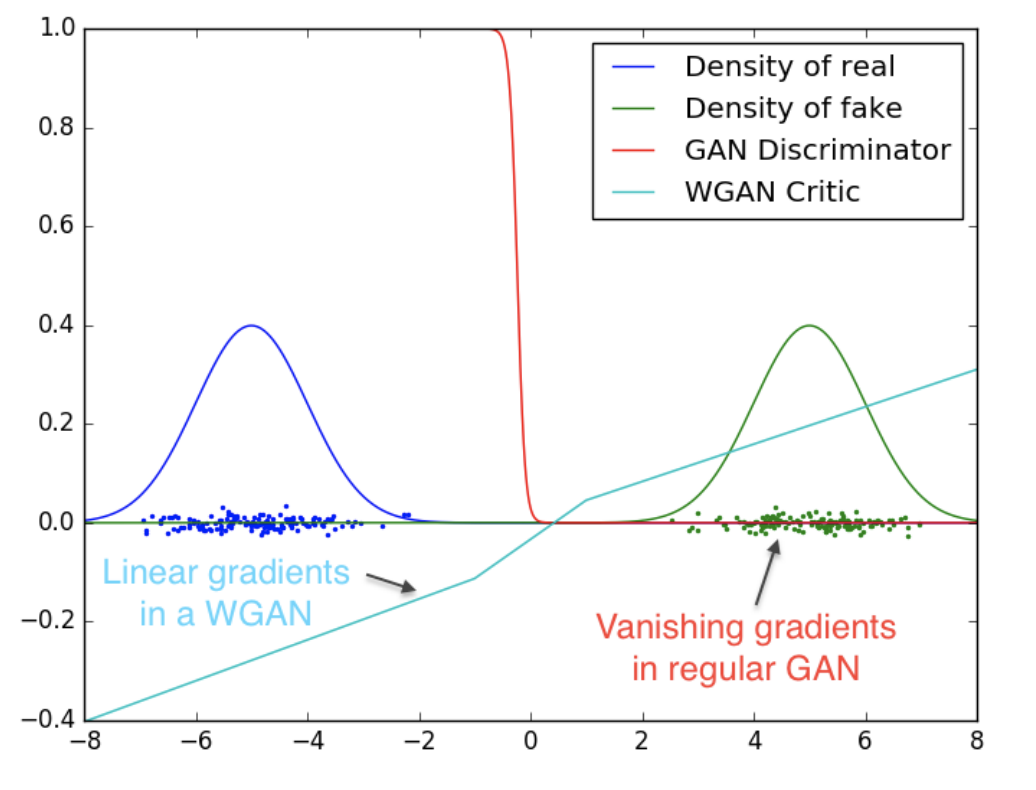
2. Ưu điểm của WGAN so với GANs truyền thống
2.1. Wasserstein distance được tính như thế nào ?
Khoảng cách Wasserstein hay còn được gọi là Earth Mover’s distance (EMD), là một thước đo sự khác biệt giữa hai phân phối xác suất. Wasserstein distance đo lường chi phí tối thiểu để biến một phân phối xác suất này thành phân phối xác suất khác, trong đó “chi phí” được tính bằng cách nhân khoảng cách cần di chuyển với khối lượng di chuyển.
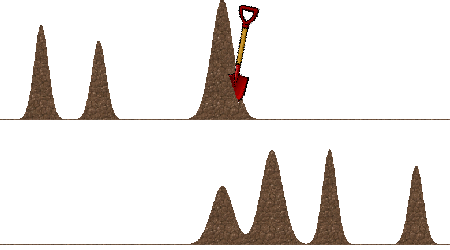
Giả sử như sau, bạn có 100 cái bánh trung thu đặt ở 4 quận: quận 1, quận 2, quận 3, quận 4 và muốn vận chuyển số bánh ở 4 quận đó sang 3 quận khác là quận 5, quận 6, và quận 7.
Vì chi phí vận chuyển dựa vào 2 yếu tố: cân nặng và quãng đường. Ta thiết lập bảng sau để đánh giá chi phí
Bảng giá chi phí quãng đường (kilometers)
| Xuất phát / Điểm đến |
Quận 1 |
Quận 2 |
Quận 3 |
Quận 4 |
| Quận 5 |
5.2 |
20.2 |
4.7 |
6.6 |
| Quận 6 |
12.2 |
24.8 |
9.1 |
11.3 |
| Quận 7 |
7.3 |
20.2 |
9.4 |
6.1 |
Phương pháp 1, ta chuyển 10 bánh ở quận 1 đến quận 5 và tất cả bánh ở quận 2 qua quận 5 cho đủ yêu cầu của quận 5. Tiếp theo, ta dùng 45 bánh ở quận 3 để đắp vào đủ số bán cho quận 6, số dư còn lại ta chuyển cho quận 7. Sau cùng, ta chuyển hết 20 bánh ở quận 4 cho quận 7 là xong. Diễn giải bằng ma trận, ta sẽ trình bày như sau.
| Xuất phát / Điểm đến |
Quận 1 (10 bánh) |
Quận 2 (5 bánh) |
Quận 3 (65 bánh) |
Quận 4 (20 bánh) |
| Quận 5 (15 bánh) |
10 |
5 |
0 |
0 |
| Quận 6 (45 bánh) |
0 |
0 |
45 |
0 |
| Quận 7 (40 bánh) |
0 |
0 |
20 |
20 |
Phương pháp 2, ta có thể vận chuyển như sau:
| Xuất phát / Điểm đến |
Quận 1 (10 bánh) |
Quận 2 (5 bánh) |
Quận 3 (65 bánh) |
Quận 4 (20 bánh) |
| Quận 5 (15 bánh) |
5 |
5 |
5 |
0 |
| Quận 6 (45 bánh) |
5 |
0 |
30 |
10 |
| Quận 7 (40 bánh) |
0 |
0 |
30 |
10 |
Với phương pháp 1, ta có chi phí được tính như sau:
\[\text{cost} = 5.2 \times 10 + 20.2*5 + 9.1 \times 45 + 9.4 \times 20 + 6.1 \times 20 = 872.5\]
Với phương pháp 2, ta có chi phí được tính toán như sau:
\[\text{cost} = 5.2 \times 5 + 12.2 \times 5 + 20.2 \times 5 + 4.7 \times 5 + 9.1 \times 30 + 9.4 \times 30 + 11.3 \times 10 + 6.1 \times 10 = 940.5\]
Note: Nếu tính tổng theo cột, ta sẽ có được tổng bánh của từng quận từ 1 tới 4. Ngược lại, nếu tính tổng theo hàng, ta sẽ có được tổng bánh của tứng quận từ 5 tới 7. Đây là một điều kiện quan trọng để phần dưới dùng để biến đổi. Đây còn gọi là marginal distributions.
Với ví dụ minh họa trên, ta thấy với mỗi lời giải ta sẽ có kết quả khác nhau và lời giải mà cho kết quả cost nhỏ nhất được định nghĩa là Wasserstein distance . Vì vậy, khoảng cách Wasserstein distance có định nghĩa toán học như sau:
\[\mathbf{W}_p(\mu, \upsilon) = (\inf_{\gamma \sim \Gamma(x, y)} \int_{\chi \times \chi} {d(x, y)^p d\gamma(x, y)})^{\frac{1}{p}} \quad \in \mathbb{R}^+\]
Với,
\[\inf: \quad \text{infinum (Giá trị nhỏ nhất)}\]
\[\chi \times \chi: \quad \text{joint probability của 2 phân phối}\]
\[\gamma: \quad \text{Transport plan}\]
\[\Gamma (x, y): \quad \text{Tập hợp tất cả các transport plans}\]
\[d(x, y): \quad \text{Chi phí khoảng cách}\]
\[d\gamma(x, y): \quad \text{Chi phí khối lượng}\]
2.2. Tại sao hàm loss của GANs truyền thống là khoảng cách Jensen-Shannon giữa phân phối của tập dữ liệu gốc và dữ liệu sinh ?
Đầu tiên, ta có hàm loss của GANs được định nghĩa như sau:
\[L(D, G) = \mathbb{E}_{x \sim P_r(x)}[log(D(x))] + \mathbb{E}_{z \sim P_z(z)}[log(1 - D(G(z)))]\]
Thay đổi, \(z\) thành biến \(x\) thuộc distribution của data được sinh \(P_g(x)\).
\[L(D, G) = \mathbb{E}_{x \sim P_r(x)}[log(D(x))] + \mathbb{E}_{x \sim P_g(x)}[log(1 - D(x))]\]
Tìm giá trị tối ưu của discriminator, vì khi đó discriminator đã không còn thể được tối ưu nữa và chúng ta chỉ cần tập trung vào generator.
\[L(D, G) = \int_{x}(P_r(x)log(D(x)) + P_g(x)log(1 - D(x)))dx\]
Thay thế \(\tilde{x} = D(x), A = P_r(x), B = P_g(x)\) vào phương trình trên, ta được cách biểu diễn mới như sau:
\[\rightarrow f(\tilde{x}) = Alog(\tilde{x}) + Blog(1 - \tilde{x})\]
Tìm \(\tilde{x}\) sao cho phương trình trên đạt điểm cực tiểu, tức discriminator đã đạt điểm tối ưu.
\[\frac{\partial f(\tilde{x})}{\partial \tilde{x}} = 0 \leftrightarrow \frac{A}{ln(10)\tilde{x}} - \frac{B}{ln(10)(1-\tilde{x})} = 0\]
\[\leftrightarrow \tilde{x} = \frac{A}{A+B} =\frac{P_r(x)}{P_r(x) + P_g(x)} \in [0, 1]\]
Khi dữ liệu sinh gần với dữ liệu gốc, \(P_g = P_r\), \(D^*(x)\) bằng \(\frac{1}{2}\). Tức nếu nhìn vào một dữ liệu sinh và dữ liệu gốc, discriminator không nhận biết được đâu là thật và đâu là giả.
Ta có định nghĩa của khoảng cách Jensen-Shannon như sau:
\[D_{JS}(P_r||P_g) = \frac{1}{2}(D_{KL}(P_r || \frac{P_r + P_g}{2}) + D_{KL}(P_g || \frac{P_r + P_g}{2}))\]
\[\leftrightarrow \frac{1}{2}(log(2) + \int_x{P_r(x)log(\frac{P_r(x)}{P_r(x) + P_g(x)})dx} + log(2) + \int_x{P_g(x)log(\frac{P_g(x)}{P_r(x) + P_g(x)})dx})\]
\[\leftrightarrow D_{JS}(P_r||P_g) = \frac{1}{2}(log(4) + L(G, D^*))\]
\[\rightarrow L(G, D^*) = 2D_{JS}(P_r||P_g) - 2log(2)\]
Với biểu diễn trên, ta thấy việc tối ưu generator (discriminator đã đạt điểm tối ưu) cũng là đang tối ưu khoảng cách Jensen-Shannon. Vì vậy, ta có thể kết luận hàm loss của GANs truyền thống là khoảng cách Jensen-Shannon giữa 2 phân phối.
2.3. Tại sao khoảng cách Wasserstein lại tốt hơn khoảng cách Kullback-Leibler, Jensen-Shannon ?
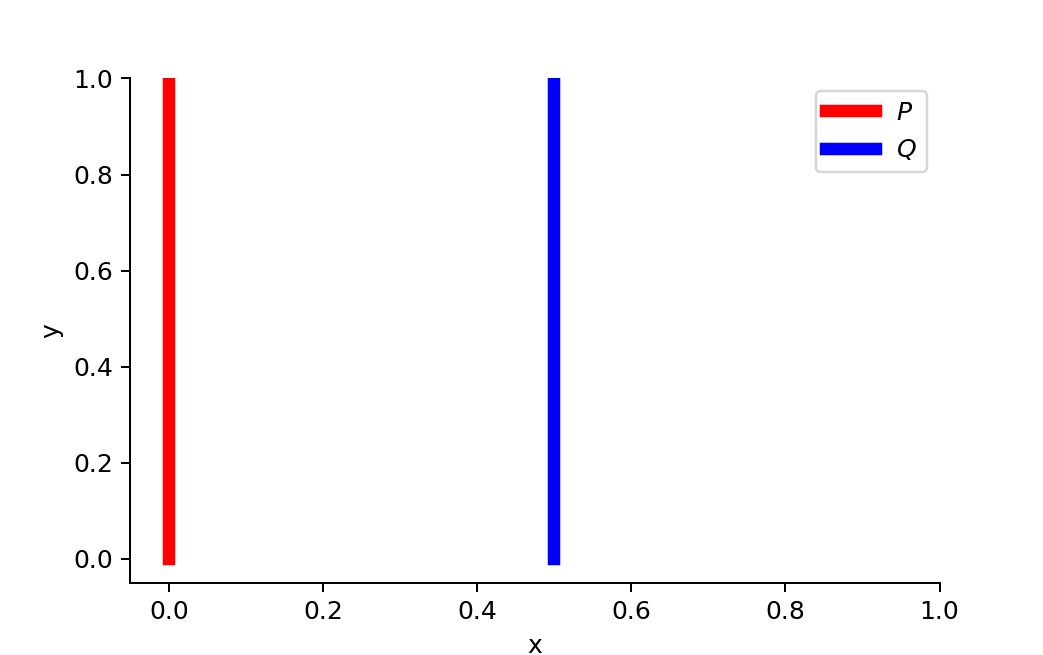
Giả sử ở trường hợp trên, distribution P nằm ở 0.0 và Q nằm ở 0.5. Với từng cách tính khoảng cách, chúng ta sẽ có được kết quả khác nhau. Cụ thể như sau:
Với khoảng cách Kullback-Leibler,
\[D_{KL}(P||Q) = \sum_{i=0}^{n}P(x_i)log(\frac{P(x_i)}{Q(x_i)}) = 1 \times log(\frac{1}{0}) + 0 \times log(\frac{0}{1}) = +\infty\]
\[D_{KL}(Q||P) = \sum_{i=0}^{n}Q(x_i)log(\frac{Q(x_i)}{P(x_i)}) = 0 \times log(\frac{0}{1}) + 1 \times log(\frac{1}{0}) = +\infty\]
Như các bạn thấy, khoảng cách Kullback-Leibler cho giá trị vô cùng và việc này sẽ dẫn tới hiện tượng exploding gradient.
Với khoảng cách Jensen-Shannon,
\[D_{JS}(P||Q) = \frac{1}{2}(D_{KL}(P||\frac{P+Q}{2}) + D_{KL}(Q||\frac{P+Q}{2}))\]
\[D_{JS}(P||Q) = \frac{1}{2}(\sum_{i=0}^{n}P(x_i)log(\frac{2P(x_i)}{P(x_i) + Q(x_i)})) + \sum_{i=0}^{n}Q(x_i)log(\frac{2Q(x_i)}{P(x_i) + Q(x_i)})\]
\[D_{JS}(P||Q) = \frac{1}{2}(1 \times log(\frac{2}{1}) + 0 \times log(\frac{0}{1}) + 0 \times log(\frac{0}{1}) + 1 \times log(\frac{2}{1})) = log(2)\]
Với cách tính của khoảng cách Jensen, dù cho distribution Q có di chuyển gần vào P hoặc xa ra P thì khoảng cách vẫn là \(log(2)\) và vì thế gradient sẽ không có sự thay đổi.
Với khoảng cách Wasserstein, nhược điểm trên được khắc phục
\[D_{Wasserstein}(P||Q) = |\theta| = d\]
Với khoảng cách Wasserstein, metric này biểu diễn rất chính xác khoảng cách của 2 distribution dù chúng nằm xa hay gần. Và dựa vào đó, chúng ta thấy sự vượt trội của khoảng cách Wasserstein so với 2 phương pháp đo khoảng cách kia.
3. Code WGAN with Pytorch
Về cơ bản, cách xây dựng generator và discriminator của WGAN giống với GAN truyền thống.
- Step 1: Import các thư viện cần thiết
import torch
from torch import nn, optim
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, Dataset
from torchvision.datasets import MNIST
import torchvision
import torch.nn.functional as F
from tqdm import tqdm
import torchvision.utils as vutils
%matplotlib inline
transform = torchvision.transforms.Compose([
torchvision.transforms.ToTensor()
])
BATCH_SIZE = 64
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
train_loader = DataLoader(MNIST("./data/", train=True, download=True, transform=transform), batch_size = BATCH_SIZE, shuffle=True)
- Step 3: Xây dựng mô hình Generator và Discriminator
Đầu tiên, ta sẽ xây dựng khối convolution gồm Conv + Batch Norm + ReLU
class Conv(nn.Module):
def __init__(self, in_channels: int, out_channels: int,
kernel_size: int = 3, stride: int = 1, padding: int =1):
super().__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, bias=False)
self.bn = nn.BatchNorm2d(out_channels)
self.act = nn.ReLU()
self.block = nn.Sequential(self.conv, self.bn, self.act)
def forward(self, x):
return self.block(x)
Sau khi có khối Conv, ta dùng nó để xây dựng discriminator và generator
class Discriminator(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = Conv(1, 16, 3, 1, 1)
self.conv2 = Conv(16, 32, 3, 1, 1)
self.conv3 = Conv(32, 64, 3, 1, 1)
self.pooling = nn.MaxPool2d(2, 2)
self.fc1 = nn.Linear(7*7*64, 1)
def forward(self, x: torch.Tensor):
x = self.conv1(x)
x = self.pooling(x)
x = self.conv2(x)
x = self.pooling(x)
x = self.conv3(x)
x = x.flatten(1)
x = self.fc1(x)
return x
class Generator(nn.Module):
def __init__(self, z_dim: int = 20):
super().__init__()
self.fc1 = nn.Linear(z_dim, 7*7*256)
self.conv1 = Conv(256, 128, 3, 1, 1)
self.conv2 = Conv(128, 64, 3, 1, 1)
self.conv3 = nn.Conv2d(64, 1, 1, 1, bias=True)
self.upsample = nn.UpsamplingBilinear2d(scale_factor=2)
def forward(self, x: torch.Tensor):
x = self.fc1(x)
x = x.reshape(-1, 256, 7, 7)
x = self.upsample(x)
x = self.conv1(x)
x = self.upsample(x)
x = self.conv2(x)
x = self.conv3(x)
x = nn.Sigmoid()(x)
return x
- Step 4: Thiết lập các optimizers, hàm train, visualise
Set up các thông số training
GEN_LR = 5e-5
DISC_LR = 5e-5
n_critic = 5
gen_optimizer = optim.Adam(generator.parameters(), lr=GEN_LR, amsgrad=True)
disc_optimizer = optim.Adam(disc.parameters(), lr=DISC_LR, amsgrad=True)
Hàm train 1 epoch
def train_1_epoch(loader, n_critic: int = 5, c: float = 0.01):
wasserstein_distance_1_epoch = 0
for real_data, _ in tqdm(loader):
real_data = real_data.to(DEVICE)
z = torch.randn((BATCH_SIZE, Z_DIM)).to(DEVICE)
generated_data = generator(z)
for _ in range(n_critic):
disc_optimizer.zero_grad()
wasserstein_distance = -(torch.mean(disc(real_data)) - torch.mean(disc(generated_data)))
wasserstein_distance.backward(retain_graph=True)
disc_optimizer.step()
for p in disc.parameters():
p.data.clamp_(-c, c)
wasserstein_distance_1_epoch -= wasserstein_distance.item()
gen_loss = -torch.mean(disc(generated_data))
gen_optimizer.zero_grad()
gen_loss.backward()
gen_optimizer.step()
return wasserstein_distance_1_epoch
Hàm visualise
@torch.no_grad()
def visualise():
generator.eval()
z = torch.randn((16, Z_DIM)).to(DEVICE)
generated_data = generator(z).cpu()
fig, ax = plt.subplots(figsize=(10, 10))
plt.axis("off")
ax.imshow(np.transpose(vutils.make_grid(generated_data, padding=2, normalize=True), (1, 2, 0)))
plt.show()
generator.train()
def train(epochs: int):
for i in range(1, epochs+1):
wasserstein_distance_1_epoch = train_1_epoch(train_loader)
print(f"Epoch: {i} Wasserstein distance of an epoch: {wasserstein_distance_1_epoch}")
visualise()
4. Giải thích đối ngẫu Kantorovich-Rubinstein
Sự khác biệt giúp WGAN vượt trội hơn GAN truyền thống đó là hàm loss. Hàm loss này giúp khắc phục điểm yếu của các phương pháp cũ và là nhân tố giúp WGAN trở thành SOTA ở thời điểm ra mắt. Tuy nhiên, hàm loss này có quá trình chứng minh và biến đổi tuy phức tạp nhưng rất thú vị. Vì vậy, chúng ta cùng tìm hiểu về đối ngẫu Kantorovich-Rubinstein, nền tảng cho Wasserstein loss nhé.
Ở trong paper, tác giả đưa ra kết quả cuối để tính Wasserstein distance như sau:
\[W(\mathbb{P_r}, \mathbb{P_\theta}) = \sup_{||f||_L \le 1} \mathbb{E_{x \sim \mathbb{P_r}}}[f(x)] - \mathbb{E_{x \sim \mathbb{P_\theta}}}[g(x)]\]
Để có thể có được kết quả cuối như trên, tác giả đã vận dụng đối ngẫu Kantorovich-Rubinstein. Đối ngẫu này được diễn giải như sau:
\[W(\mathbb{P_r}, \mathbb{P_g}) = \inf_{\gamma \in \Pi (\mathbb{P_r}, \mathbb{P_g})}{\mathbb{E}_{(x, y) \sim \gamma}[||x-y||]}\]
Với 2 marginal constraints:
\[\mathbb{P}_r(x) = \int_{\chi} d\gamma(x, y)dy\]
\[\mathbb{P}_g(y) = \int_{\chi} d\gamma(x, y)dx\]
Áp dụng Larange multipliers, ta được hàm tối ưu như sau:
\[L(\pi, f, g) = \int_{\chi \times \chi}||x-y|| \pi(x, y)dxdy + \int_{\chi}(\mathbb{P}_r(x) - \int_{\chi}\pi(x, y)dy)f(x)dx + \int_{\chi}(\mathbb{P}_g(y) - \int_{\chi}\pi(x, y)dx)g(y)dy\]
\[L(\pi, f, g) = \mathbb{E_{x \sim \mathbb{P}_r(x)}}[f(x)] + \mathbb{E_{y \sim \mathbb{P}_g(y)}}[g(y)] + \int_{\chi \times \chi}(||x-y|| - f(x) - g(y)) \pi(x, y)dxdy\]
Ta có khoảng cách Wasserstein được định nghĩa như sau:
\[W(\mathbb{P_r}, \mathbb{P_\theta}) = \inf_{\pi} \sup_{f, g} L(\pi, f, g)\]
Vì khoảng cách Wasserstein là hàm lồi convex và chắc chắn có nghiệm nên nó thỏa đối ngẫu mạnh (strong duality).
Biến đổi đối ngẫu, ta được:
\[W(\mathbb{P_r}, \mathbb{P_\theta}) = \inf_{\pi} \sup_{f, g} L(\pi, f, g) = \sup_{f, g} \inf_{\pi} L(\pi, f, g)\]
\[W(\mathbb{P_r}, \mathbb{P_\theta}) = \sup_{f, g} \inf_{\pi} \mathbb{E_{x \sim \mathbb{P}_r(x)}}[f(x)] + \mathbb{E_{y \sim \mathbb{P}_g(y)}}[g(y)] + \int_{\chi \times \chi}(||x-y|| - f(x) - g(y)) \pi(x, y)dxdy\]
Ở phương trình trên, ta có 2 expections độc lập với \(\pi\) nên có thể rút ra ngoài.
\[W(\mathbb{P_r}, \mathbb{P_\theta}) = \sup_{f, g} \mathbb{E_{x \sim \mathbb{P}_r(x)}}[f(x)] + \mathbb{E_{y \sim \mathbb{P}_g(y)}}[g(y)] + \inf_{\pi} \int_{\chi \times \chi}(||x-y|| - f(x) - g(y)) \pi(x, y)dxdy\]
Đối với vế sau của phương trình,
\[\inf_{\pi} \int_{\chi \times \chi}(||x-y|| - f(x) - g(y)) \pi(x, y)dxdy = 0 \quad \text{if } ||x-y|| \ge f(x) + g(y)\]
Áp dụng điều kiện trên, ta được:
\[W(p, p_g) = \sup_{\substack{f, g \\ f(x) + g(y) \leq ||x - y||}} L(\pi, f, g) = \sup_{\substack{f, g \\ f(x) + g(y) \leq ||x - y||}} \mathbb{E_{x \sim \mathbb{P}_r(x)}}[f(x)] + \mathbb{E_{y \sim \mathbb{P}_g(y)}}[g(y)]\]
Tới đây, chúng ta đã có thể thay hàm neural networks vào \(f\) và \(g\) hoặc cho chúng cùng params để có thể tính được khoảng cách Wasserstein. Tuy nhiên, có một rào cản khiến cho việc này khó khả thi.
Giả sử, mình sẽ đặt \(g = f\) và được parameterised \(g_\phi = f_\phi\). Biến đổi phương trình trên, ta được:
\[W(p, p_g) = \sup_{\substack{f, g \\ f_\phi(x) + f_\phi(y) \leq ||x - y||}} \mathbb{E_{x \sim \mathbb{P}_r(x)}}[f_\phi(x)] + \mathbb{E_{y \sim \mathbb{P}_g(y)}}[f_\phi(y)]\]
Rào cản khiến cho việc biến đổi đến đây vẫn chưa thể tính được khoảng cách Wasserstein là ràng buộc
\(f_\phi(x) + f_\phi(y) \leq ||x - y||\)
. Ở thời điểm hiện tại, việc implement một mạng neural network để có thể giống như ràng buộc trên là rất khó. Vì vậy, chúng ta sẽ tiếp tục biến đổi với mong muốn có được một dạng ràng buộc nào đó có thể dễ xấp xỉ bằng mạng neural network hơn.
Định lý Kantorovich-Rubinstein đề xuất “infimal convolution”, nó được định nghĩa như sau:
\[\kappa(x) = \inf_{u}\{||x-u|| - g(u)\}\]
Với việc định nghĩa hàm \(\kappa(x)\), định lý này chứng minh đây là hàm 1-Lipschitz như sau:
\[\kappa(x) \leq ||x-u|| - g(u) \leq ||x-y|| + ||y-u|| - g(u) \quad \text{(Định lý hình tam giác)}\]
\[\Leftrightarrow \kappa(x) \leq ||x-y|| + \inf_{u}\{||y-u|| - g(u)\} \leq ||x-y|| + \kappa(y)\]
\[\Leftrightarrow \kappa(x) - \kappa(y) \leq ||x-y||\]
Đổi lại thứ tự biến \(x\) và \(y\), ta được
\[\Leftrightarrow \kappa(y) - \kappa(x) \leq ||x-y||\]
Vì vậy ta có thể kết luận hàm \(\kappa\) là hàm 1-Lipschitz.
Bây giờ chúng ta sẽ biến đổi ràng buộc
\(f(x) + g(y) \leq ||x - y||\)
sang một biểu thức đơn giản để tính hơn như sau:
Ta có:
\[f(x) + g(y) \leq ||x - y||\]
\[\Leftrightarrow f(x) \leq ||x - y|| - g(y)\]
\[\Leftrightarrow f(x) = \inf_{y}\{||x - y|| - g(y)\} = \kappa(x)\]
\[\kappa(y) \leq ||y - y|| - g(y) = -g(y)\]
\[\rightarrow g(y) \leq -\kappa(y)\]
Áp dụng 2 phương trình trên vào, ta được:
\[\mathbb{E_{x \sim p}}[f(x)] + \mathbb{E_{y \sim q}}[g(y)] \leq \mathbb{E_{x \sim \mathbb{P}_r(x)}}[\kappa(x)] - \mathbb{E_{y \sim \mathbb{P}_g(y)}}[\kappa(y)]\]
Tổng kết lại, chúng ta sẽ có được phương trình tối ưu cuối cùng như sau:
\[W(p, p_g) \leq \sup_{\substack{\kappa \\ ||\kappa||_L \leq 1}} \mathbb{E_{x \sim \mathbb{P}_r(x)}}[\kappa(x)] - \mathbb{E_{y \sim \mathbb{P}_g(y)}}[\kappa(y)]\]
Và đây là hàm chúng ta dùng để tối ưu model, vì chúng ta chỉ quan tâm tới việc tối thiểu hàm loss nên sẽ không thật sự cần tính đúng khoảng cách Wasserstein, chỉ cần tìm được cận trên hoặc cận dưới là đủ.
5. Điểm yếu còn tồn đọng của WGAN
Như các bạn thấy ở trên, tác giải sử dụng phương pháp weight clipping để làm cho mạng discriminator behave giống hàm 1-Lipschitz nhất có thể. Tuy nhiên cách này không đúng và phụ thuộc khá nhiều vào hyperparameter c, tác giả cũng thừa nhận trong paper “Weight clipping is a clearly terrible way to enforce a Lipschitz constraint”. Nếu muốn hệ số c lớn hơn, ta phải đánh đổi bằng việc sử dụng mạng discriminator lớn hơn và hội tụ chậm hơn, ngược lại, nếu c nhỏ hơn thì hội tụ sẽ nhanh hơn nhưng sẽ bị vanishing gradient.
6. Kết luận
Mô hình WGAN đã gây ra tiếng vang rất lớn khi vừa được ra mắt. Tưởng chừng như đã thay đổi cuộc cách mạng GANs-based generative AI nhưng dường như nó vẫn bị kìm hàm bởi các điểm yếu được liệt kê ở trên. Tuy mặc dù đa số mô hình GANs hiện tại vẫn dùng hàm loss truyền thống, cách thức tiếp cận vấn đề của WGAN vẫn là rất tiềm năng và đáng học hỏi.
Mình đã giới thiệu về WGAN, cách hoạt động, cũng như code from scratch mô hình này. Nếu có thắc mắc, hãy gửi về email cá nhân của mình và mình sẽ giải đáp. Chúc các bạn học tốt, peace.
References
1. Wasserstein GAN - arXiv
2. Wasserstein GAN and the Kantorovich-Rubinstein Duality
3. Kantorovich-Rubinstein Duality
4. Introduction to the Wasserstein distance - Youtube
5. From GAN to WGAN